Sines Law , Componendo and Dividendo

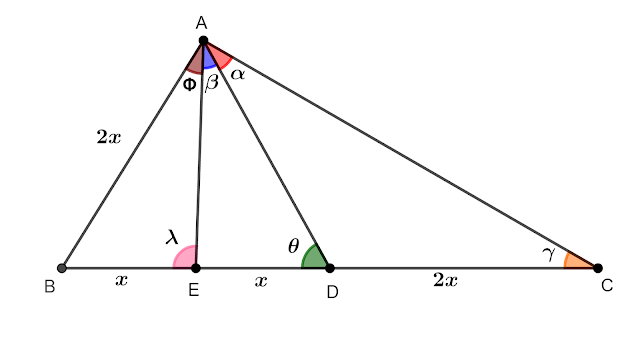
ABC is a triangle having  BC = 2 AB . Bisect  BC  in  D  and  BD  in  E .
Prove that  AD  bisects  $\displaystyle \angle \ CAE.$

Solution

$\displaystyle \text{Let}\ AB=2x$

$\displaystyle \ \ \ \therefore \ BC=4x\ \ \ \left( {\because \ BC=2AB} \right)$

$\displaystyle \text{Bisect}\ BC\ \ \text{in}\ \ D\ \ \text{and}\ \ BD\ \ \text{in}\ \ E\ .\ \ \left( {\text{Given}} \right)$ 

$\displaystyle BD=DC=2x\ and\ \ BE=ED=x$

By the law of sines ,

$\displaystyle \frac{{AB}}{{\sin \gamma }}=\frac{{BC}}{{\sin \left( {\phi +\beta +\alpha } \right)}}$ 

$\displaystyle \frac{{2x}}{{\sin \left( {\theta -\alpha } \right)}}=\frac{{4x}}{{\sin \left( {\theta +\alpha } \right)}}$

$\displaystyle \frac{{\sin \left( {\theta +\alpha } \right)}}{{\sin \left( {\theta -\alpha } \right)}}=2\ \ \ \ ...........(1)$

$\displaystyle \frac{{BE}}{{\sin \phi }}=\frac{{AB}}{{\sin \lambda }}$

$\displaystyle \frac{x}{{\sin \left( {\theta -\beta } \right)}}=\frac{{2x}}{{\sin \left( {\theta +\beta } \right)}}$

$\displaystyle \frac{{\sin \left( {\theta +\beta } \right)}}{{\sin \left( {\theta -\beta } \right)}}=2\ \ \ \ ...........(2)$

$\displaystyle \text{From}\ (1)\ \text{and}\ (2)\ ,$

$\displaystyle \frac{{\sin \left( {\theta +\alpha } \right)}}{{\sin \left( {\theta -\alpha } \right)}}=\frac{{\sin \left( {\theta +\beta } \right)}}{{\sin \left( {\theta -\beta } \right)}}$

$\displaystyle \text{By}\ \text{Componendo}\ \And \ \text{Dividendo}\ ,$

$\displaystyle \frac{{\sin \left( {\theta +\alpha } \right)+\sin \left( {\theta -\alpha } \right)}}{{\sin \left( {\theta +\alpha } \right)-\sin \left( {\theta -\alpha } \right)}}=\frac{{\sin \left( {\theta +\beta } \right)+\sin \left( {\theta -\beta } \right)}}{{\sin \left( {\theta +\beta } \right)-\sin \left( {\theta -\beta } \right)}}$

$\displaystyle \frac{{2\sin \theta \cos \alpha }}{{2\cos \theta \sin \alpha }}=\frac{{2\sin \theta \cos \beta }}{{2\cos \theta \sin \beta }}$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \cot \alpha =\cot \beta $

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \alpha =\beta $

$\displaystyle \therefore \ AD\ \text{bisects}\ \angle \ CAE.$