Sines Law , Componendo and Dividendo

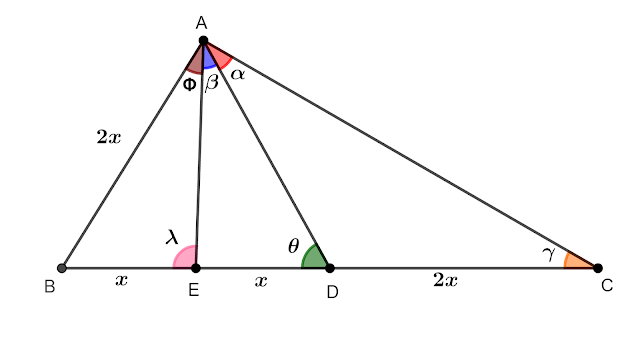
ABC is a triangle having  BC = 2 AB . Bisect  BC  in  D  and  BD  in  E .
Prove that  AD  bisects  $\displaystyle \angle \ CAE.$

Solution

$\displaystyle \text{Let}\ AB=2x$

$\displaystyle \ \ \ \therefore \ BC=4x\ \ \ \left( {\because \ BC=2AB} \right)$

$\displaystyle \text{Bisect}\ BC\ \ \text{in}\ \ D\ \ \text{and}\ \ BD\ \ \text{in}\ \ E\ .\ \ \left( {\text{Given}} \right)$ 

$\displaystyle BD=DC=2x\ and\ \ BE=ED=x$

By the law of sines ,

$\displaystyle \frac{{AB}}{{\sin \gamma }}=\frac{{BC}}{{\sin \left( {\phi +\beta +\alpha } \right)}}$ 

$\displaystyle \frac{{2x}}{{\sin \left( {\theta -\alpha } \right)}}=\frac{{4x}}{{\sin \left( {\theta +\alpha } \right)}}$

$\displaystyle \frac{{\sin \left( {\theta +\alpha } \right)}}{{\sin \left( {\theta -\alpha } \right)}}=2\ \ \ \ ...........(1)$

$\displaystyle \frac{{BE}}{{\sin \phi }}=\frac{{AB}}{{\sin \lambda }}$

$\displaystyle \frac{x}{{\sin \left( {\theta -\beta } \right)}}=\frac{{2x}}{{\sin \left( {\theta +\beta } \right)}}$

$\displaystyle \frac{{\sin \left( {\theta +\beta } \right)}}{{\sin \left( {\theta -\beta } \right)}}=2\ \ \ \ ...........(2)$

$\displaystyle \text{From}\ (1)\ \text{and}\ (2)\ ,$

$\displaystyle \frac{{\sin \left( {\theta +\alpha } \right)}}{{\sin \left( {\theta -\alpha } \right)}}=\frac{{\sin \left( {\theta +\beta } \right)}}{{\sin \left( {\theta -\beta } \right)}}$

$\displaystyle \text{By}\ \text{Componendo}\ \And \ \text{Dividendo}\ ,$

$\displaystyle \frac{{\sin \left( {\theta +\alpha } \right)+\sin \left( {\theta -\alpha } \right)}}{{\sin \left( {\theta +\alpha } \right)-\sin \left( {\theta -\alpha } \right)}}=\frac{{\sin \left( {\theta +\beta } \right)+\sin \left( {\theta -\beta } \right)}}{{\sin \left( {\theta +\beta } \right)-\sin \left( {\theta -\beta } \right)}}$

$\displaystyle \frac{{2\sin \theta \cos \alpha }}{{2\cos \theta \sin \alpha }}=\frac{{2\sin \theta \cos \beta }}{{2\cos \theta \sin \beta }}$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \cot \alpha =\cot \beta $

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \alpha =\beta $

$\displaystyle \therefore \ AD\ \text{bisects}\ \angle \ CAE.$

Solving problem with compound angle formula

$\displaystyle A+B+C={{180}^{\circ }}$

$\displaystyle 3\sin A+4\cos B=6$

$\displaystyle 3\cos A+4\sin B=\sqrt{{13}}$

$\displaystyle \sin x=?$

$\displaystyle \text{Solution}$

$\displaystyle A+B+C={{180}^{\circ }}$ 

$\displaystyle 3\sin A+4\cos B=6$ 

$\displaystyle {{\left( {3\sin A+4\cos B} \right)}^{2}}={{6}^{2}}$

$\displaystyle 9{{\sin }^{2}}A+24\sin A\cos B+16{{\cos }^{2}}B=36\ ..........(1)$

$\displaystyle 3\cos A+4\sin B=\sqrt{{13}}$

$\displaystyle {{\left( {3\cos A+4\sin B} \right)}^{2}}={{\left( {\sqrt{{13}}} \right)}^{2}}$ 

$\displaystyle 9{{\cos }^{2}}A+24\cos A\sin B+16{{\sin }^{2}}B=13\ ............(2)$ 

$\displaystyle (1)+(2)\Rightarrow \ $

$\displaystyle 9\left( {{{{\sin }}^{2}}A+{{{\cos }}^{2}}A} \right)+24\left( {\sin A\cos B+\cos A\sin B} \right)+16\left( {{{{\sin }}^{2}}B+{{{\cos }}^{2}}B} \right)=49$

$\displaystyle \ 9+24\sin \left( {A+B} \right)+16=49$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ 24\sin \left( {A+B} \right)=24$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sin \left( {A+B} \right)=1$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \sin \left( {{{{180}}^{\circ }}-C} \right)=1$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore \ \ \sin C=1$

Solving problem with Factor and sum formulae

$\displaystyle \text{Prove}\ \text{that}\ \ \ \frac{{\cos 8x-\cos 7x}}{{1+2\cos 5x}}=\cos 3x-\cos 2x\ .$

Solution

$\displaystyle \ \ \ \frac{{\cos 8x-\cos 7x}}{{1+2\cos 5x}}=\frac{{-2\sin \frac{{15x}}{2}\sin \frac{x}{2}}}{{1+2\left( {2{{{\cos }}^{2}}\frac{{5x}}{2}-1} \right)}}$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{-2\sin \frac{{15x}}{2}\sin \frac{x}{2}}}{{4{{{\cos }}^{2}}\frac{{5x}}{2}-1}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{-2\sin \frac{{15x}}{2}\sin \frac{x}{2}}}{{4{{{\cos }}^{2}}\frac{{5x}}{2}-1}}\ \ \times \ \ \frac{{-2{{{\sin }}^{2}}\frac{{5x}}{2}}}{{-2{{{\sin }}^{2}}\frac{{5x}}{2}}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\left( {-2\sin \frac{{5x}}{2}\sin \frac{x}{2}} \right)\left( {-2\sin \frac{{15x}}{2}\sin \frac{{5x}}{2}} \right)}}{{2{{{\sin }}^{2}}\frac{{5x}}{2}-8{{{\sin }}^{2}}\frac{{5x}}{2}{{{\cos }}^{2}}\frac{{5x}}{2}}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\left( {\cos 3x-\cos 2x} \right)\left( {\cos 10x-\cos 5x} \right)}}{{2{{{\sin }}^{2}}\frac{{5x}}{2}-2{{{\left( {2\sin \frac{{5x}}{2}\cos \frac{{5x}}{2}} \right)}}^{2}}}}$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\left( {\cos 3x-\cos 2x} \right)\left( {\cos 10x-\cos 5x} \right)}}{{2{{{\sin }}^{2}}\frac{{5x}}{2}-2{{{\sin }}^{2}}5x}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\left( {\cos 3x-\cos 2x} \right)\left( {\cos 10x-\cos 5x} \right)}}{{\left( {1-\cos 5x} \right)-\left( {1-\cos 10x} \right)}}\ \ \ \ \ \ \left[ {\because \cos 2\theta =1-2{{{\sin }}^{2}}\theta } \right]$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\left( {\cos 3x-\cos 2x} \right)\left( {\cos 10x-\cos 5x} \right)}}{{\cos 10x-\cos 5x}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\cos 3x-\cos 2x$

Solving problem with Sines law and Cosines law

In the diagram below , the lengths of the three sides of the triangle are $\displaystyle a\ cm\ ,\ b\ cm\ \text{and}\ c\ cm$ . It is given that $\displaystyle \frac{{{{a}^{2}}+{{b}^{2}}}}{{{{c}^{2}}}}=2011$ . Find the value of $\displaystyle \frac{{\cot C}}{{\cot A\ +\ \cot B}}$ .

Solution

$\displaystyle \frac{{{{a}^{2}}+{{b}^{2}}}}{{{{c}^{2}}}}=2011$

$\displaystyle {{a}^{2}}+{{b}^{2}}=2011\ {{c}^{2}}$

$\displaystyle {{a}^{2}}+{{b}^{2}}-{{c}^{2}}=2010\ {{c}^{2}}$

$\displaystyle \frac{{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}}{{2ab}}=\frac{{2010\ {{c}^{2}}}}{{2ab}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \cos C=\frac{{2010\ {{c}^{2}}}}{{2ab}}\ \ \ \ \ \ \ \ \ \ \ \ \ \left[ {\because \cos C=\frac{{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}}{{2ab}}} \right]$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \cos C=1005\left( {\frac{c}{a}} \right)\left( {\frac{c}{b}} \right)$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \cos C=1005\left( {\frac{{\sin C}}{{\sin A}}} \right)\left( {\frac{{\sin C}}{{\sin B}}} \right)\ \ \ \left[ {\because \ \frac{a}{{\sin A}}=\frac{b}{{\sin B}}=\frac{c}{{\sin C}}} \right]$

$\displaystyle \ \ \ \ \ \ \ \ \ \frac{{\cos C}}{{\sin C}}=\frac{{1005\sin C}}{{\sin A\ \sin B}}$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \cot C=\frac{{1005\sin \left( {{{{180}}^{\circ }}-\left( {A+B} \right)} \right)}}{{\sin A\ \sin B}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \cot C=\frac{{1005\sin \left( {A+B} \right)}}{{\sin A\ \sin B}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \cot C=1005\left( {\frac{{\sin A\ \cos B+\cos A\ \sin B}}{{\sin A\ \sin B}}} \right)$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \cot C=1005\left( {\frac{{\sin A\ \cos B}}{{\sin A\ \sin B}}+\frac{{\cos A\ \sin B}}{{\sin A\ \sin B}}} \right)$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \cot C=1005\left( {\cot B+\cot A} \right)$ 

$\displaystyle \therefore \ \frac{{\cot C}}{{\cot A\ +\ \cot B}}=1005$

Solving problem with double angle formula and factor formula

Find the value of
$\displaystyle (\ \text{i}\ )\ \ \ {{\sin }^{4}}\frac{\pi }{8}+{{\cos }^{4}}\frac{\pi }{8}+{{\sin }^{4}}\frac{{7\pi }}{8}+{{\cos }^{4}}\frac{{7\pi }}{8}$

$\displaystyle (\ ii\ )\ \frac{3}{{{{{\sin }}^{2}}{{{20}}^{\circ }}}}-\frac{1}{{{{{\cos }}^{2}}{{{20}}^{\circ }}}}+64{{\sin }^{2}}{{20}^{\circ }}$

Solution

$\displaystyle (\ \text{i}\ )\ \ \ {{\sin }^{4}}\frac{\pi }{8}+{{\cos }^{4}}\frac{\pi }{8}+{{\sin }^{4}}\frac{{7\pi }}{8}+{{\cos }^{4}}\frac{{7\pi }}{8}$

$\displaystyle \ \ \ \ \ ={{\left( {{{{\sin }}^{2}}\frac{\pi }{8}+{{{\cos }}^{2}}\frac{\pi }{8}} \right)}^{2}}-2{{\sin }^{2}}\frac{\pi }{8}{{\cos }^{2}}\frac{\pi }{8}+{{\left( {{{{\sin }}^{2}}\frac{{7\pi }}{8}+{{{\cos }}^{2}}\frac{{7\pi }}{8}} \right)}^{2}}-2{{\sin }^{2}}\frac{{7\pi }}{8}{{\cos }^{2}}\frac{{7\pi }}{8}$ 

$\displaystyle \ \ \ \ \ =1-\frac{1}{2}{{\left( {2\sin \frac{\pi }{8}\cos \frac{\pi }{8}} \right)}^{2}}+1-\frac{1}{2}{{\left( {2\sin \frac{{7\pi }}{8}\cos \frac{{7\pi }}{8}} \right)}^{2}}$ 

$\displaystyle \ \ \ \ \ =2-\frac{1}{2}{{\sin }^{2}}\frac{\pi }{4}-\frac{1}{2}{{\sin }^{2}}\frac{{7\pi }}{4}$

$\displaystyle \ \ \ \ \ =2-\frac{1}{2}\left( {{{{\sin }}^{2}}\frac{\pi }{4}+{{{\sin }}^{2}}\frac{{7\pi }}{4}} \right)$

$\displaystyle \ \ \ \ \ =2-\frac{1}{2}\left( {{{{\sin }}^{2}}\frac{\pi }{4}+{{{\sin }}^{2}}\left( {2\pi -\frac{\pi }{4}} \right)} \right)$

$\displaystyle \ \ \ \ \ =2-\frac{1}{2}\left( {{{{\sin }}^{2}}\frac{\pi }{4}+{{{\sin }}^{2}}\frac{\pi }{4}} \right)\ \ \ \ \left[ {\because \sin \left( {2\pi -\theta } \right)=-\sin \theta \ ,\ {{{\sin }}^{2}}\left( {2\pi -\theta } \right)={{{\sin }}^{2}}\theta } \right]$

$\displaystyle \ \ \ \ \ =2-{{\sin }^{2}}\frac{\pi }{4}$

$\displaystyle \ \ \ \ \ =2-\frac{1}{2}=\frac{3}{2}$ 

$\displaystyle (\ ii\ )\ \frac{3}{{{{{\sin }}^{2}}{{{20}}^{\circ }}}}-\frac{1}{{{{{\cos }}^{2}}{{{20}}^{\circ }}}}+64{{\sin }^{2}}{{20}^{\circ }}$ 

$\displaystyle \ \ \ \ =\frac{{3{{{\cos }}^{2}}{{{20}}^{\circ }}-{{{\sin }}^{2}}{{{20}}^{\circ }}+64{{{\sin }}^{4}}{{{20}}^{\circ }}{{{\cos }}^{2}}{{{20}}^{\circ }}}}{{{{{\sin }}^{2}}{{{20}}^{\circ }}{{{\cos }}^{2}}{{{20}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ =\frac{{3\left( {1-{{{\sin }}^{2}}{{{20}}^{\circ }}} \right)-{{{\sin }}^{2}}{{{20}}^{\circ }}+16{{{\sin }}^{2}}{{{20}}^{\circ }}\left( {4{{{\sin }}^{2}}{{{20}}^{\circ }}{{{\cos }}^{2}}{{{20}}^{\circ }}} \right)}}{{\frac{1}{4}\left( {4{{{\sin }}^{2}}{{{20}}^{\circ }}{{{\cos }}^{2}}{{{20}}^{\circ }}} \right)}}$

$\displaystyle \ \ \ \ =\frac{{3-3{{{\sin }}^{2}}{{{20}}^{\circ }}-{{{\sin }}^{2}}{{{20}}^{\circ }}+16{{{\sin }}^{2}}{{{20}}^{\circ }}{{{\left( {2\sin {{{20}}^{\circ }}\cos {{{20}}^{\circ }}} \right)}}^{2}}}}{{\frac{1}{4}{{{\left( {2\sin {{{20}}^{\circ }}\cos {{{20}}^{\circ }}} \right)}}^{2}}}}$

$\displaystyle \ \ \ \ =\frac{{3-4{{{\sin }}^{2}}{{{20}}^{\circ }}+16{{{\sin }}^{2}}{{{20}}^{\circ }}{{{\sin }}^{2}}{{{40}}^{\circ }}}}{{\frac{1}{4}{{{\sin }}^{2}}{{{40}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ =\frac{{3-4{{{\sin }}^{2}}{{{20}}^{\circ }}+{{{\left( {4\sin {{{40}}^{\circ }}\sin {{{20}}^{\circ }}} \right)}}^{2}}}}{{\frac{1}{4}{{{\sin }}^{2}}{{{40}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ =\frac{{3-4{{{\sin }}^{2}}{{{20}}^{\circ }}+{{{\left( {2\left( {\cos {{{20}}^{\circ }}-\cos {{{60}}^{\circ }}} \right)} \right)}}^{2}}}}{{\frac{1}{4}{{{\sin }}^{2}}{{{40}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ =\frac{{3-4{{{\sin }}^{2}}{{{20}}^{\circ }}+4{{{\left( {\cos {{{20}}^{\circ }}-\cos {{{60}}^{\circ }}} \right)}}^{2}}}}{{\frac{1}{4}{{{\sin }}^{2}}{{{40}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ =\frac{{12-16{{{\sin }}^{2}}{{{20}}^{\circ }}+16{{{\left( {\cos {{{20}}^{\circ }}-\frac{1}{2}} \right)}}^{2}}}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}$

$\displaystyle \ \ \ \ =\frac{{12-16{{{\sin }}^{2}}{{{20}}^{\circ }}+16\left( {{{{\cos }}^{2}}{{{20}}^{\circ }}-\cos {{{20}}^{\circ }}+\frac{1}{4}} \right)}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}$

$\displaystyle \ \ \ \ =\frac{{12-16{{{\sin }}^{2}}{{{20}}^{\circ }}+16{{{\cos }}^{2}}{{{20}}^{\circ }}-16\cos {{{20}}^{\circ }}+4}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}$

$\displaystyle \ \ \ \ =\frac{{16\left( {1+{{{\cos }}^{2}}{{{20}}^{\circ }}-{{{\sin }}^{2}}{{{20}}^{\circ }}-\cos {{{20}}^{\circ }}} \right)}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ =\frac{{16\left( {1+\cos {{{40}}^{\circ }}-\cos {{{20}}^{\circ }}} \right)}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}$

$\displaystyle \ \ \ \ =\frac{{16\left( {1-2\sin {{{30}}^{\circ }}\sin {{{10}}^{\circ }}} \right)}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}$

$\displaystyle \ \ \ \ =\frac{{16\left( {\sin {{{90}}^{\circ }}-\sin {{{10}}^{\circ }}} \right)}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}$

$\displaystyle \ \ \ \ =\frac{{32\cos {{{50}}^{\circ }}\sin {{{40}}^{\circ }}}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ =\frac{{32{{{\sin }}^{2}}{{{40}}^{\circ }}}}{{{{{\sin }}^{2}}{{{40}}^{\circ }}}}\ \ \ \ \ \left[ {\because \cos {{{50}}^{\circ }}=\sin {{{40}}^{\circ }}} \right]$

$\displaystyle \ \ \ \ =32$

Solving problem with compound angle formula

Find the value of
$\displaystyle (\ \text{i}\ )\ \ \ \ \frac{{\sin {{{80}}^{\circ }}}}{{\sin {{{20}}^{\circ }}}}-\frac{{\sqrt{3}}}{{2\sin {{{80}}^{\circ }}}}$

$\displaystyle (\ \text{ii}\ )\ \ \ \ \left( {\cot {{{25}}^{\circ }}-1} \right)\left( {\cot {{{24}}^{\circ }}-1} \right)\left( {\cot {{{20}}^{\circ }}-1} \right)\left( {\cot {{{21}}^{\circ }}-1} \right)$

Solution

$\displaystyle (\ \text{i}\ )\ \ \ \ \frac{{\sin {{{80}}^{\circ }}}}{{\sin {{{20}}^{\circ }}}}-\frac{{\sqrt{3}}}{{2\sin {{{80}}^{\circ }}}}$

$\displaystyle \ \ \ \ \ \ =\frac{{\cos {{{10}}^{\circ }}}}{{2\sin {{{10}}^{\circ }}\cos {{{10}}^{\circ }}}}-\frac{{\sqrt{3}}}{{2\cos {{{10}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ \ \ =\frac{1}{{2\sin {{{10}}^{\circ }}}}-\frac{{\sqrt{3}}}{{2\cos {{{10}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ \ \ =\frac{{\frac{1}{2}}}{{\sin {{{10}}^{\circ }}}}-\frac{{\frac{{\sqrt{3}}}{2}}}{{\cos {{{10}}^{\circ }}}}$

$\displaystyle \ \ \ \ \ \ =\frac{{\sin {{{30}}^{\circ }}}}{{\sin {{{10}}^{\circ }}}}-\frac{{\cos {{{30}}^{\circ }}}}{{\cos {{{10}}^{\circ }}}}$

$\displaystyle \ \ \ \ \ \ =\frac{{\sin {{{30}}^{\circ }}\cos {{{10}}^{\circ }}-\cos {{{30}}^{\circ }}\sin {{{10}}^{\circ }}}}{{\sin {{{10}}^{\circ }}\cos {{{10}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ \ \ =\frac{{\sin \left( {{{{30}}^{\circ }}-{{{10}}^{\circ }}} \right)}}{{\sin {{{10}}^{\circ }}\cos {{{10}}^{\circ }}}}$

$\displaystyle \ \ \ \ \ \ =\frac{{\sin {{{20}}^{\circ }}}}{{\sin {{{10}}^{\circ }}\cos {{{10}}^{\circ }}}}$

$\displaystyle \ \ \ \ \ \ =\frac{{2\sin {{{10}}^{\circ }}\cos {{{10}}^{\circ }}}}{{\sin {{{10}}^{\circ }}\cos {{{10}}^{\circ }}}}$ 

$\displaystyle \ \ \ \ \ \ =2$ 

$\displaystyle (\ \text{ii}\ )\ \ \ \ \left( {\cot {{{25}}^{\circ }}-1} \right)\left( {\cot {{{24}}^{\circ }}-1} \right)\left( {\cot {{{20}}^{\circ }}-1} \right)\left( {\cot {{{21}}^{\circ }}-1} \right)$ 

$\displaystyle \ \ \ \ \ \ \ =\left( {\frac{1}{{\tan {{{25}}^{\circ }}}}-1} \right)\left( {\frac{1}{{\tan {{{24}}^{\circ }}}}-1} \right)\left( {\frac{1}{{\tan {{{20}}^{\circ }}}}-1} \right)\left( {\frac{1}{{\tan {{{21}}^{\circ }}}}-1} \right)$

$\displaystyle \ \ \ \ \ \ \ =\left( {\frac{{1-\tan {{{25}}^{\circ }}}}{{\tan {{{25}}^{\circ }}}}} \right)\left( {\frac{{1-\tan {{{24}}^{\circ }}}}{{\tan {{{24}}^{\circ }}}}} \right)\left( {\frac{{1-\tan {{{20}}^{\circ }}}}{{\tan {{{20}}^{\circ }}}}} \right)\left( {\frac{{1-\tan {{{21}}^{\circ }}}}{{\tan {{{21}}^{\circ }}}}} \right)$

$\displaystyle \ \ \ \ \ \ \ =\left( {\frac{{\left( {1-\tan {{{25}}^{\circ }}} \right)\left( {1-\tan {{{20}}^{\circ }}} \right)}}{{\tan {{{25}}^{\circ }}\tan {{{20}}^{\circ }}}}} \right)\left( {\frac{{\left( {1-\tan {{{24}}^{\circ }}} \right)\left( {1-\tan {{{21}}^{\circ }}} \right)}}{{\tan {{{24}}^{\circ }}\tan {{{21}}^{\circ }}}}} \right)$

$\displaystyle \ \ \ \ \ \ \ =\left( {\frac{{1-\tan {{{20}}^{\circ }}-\tan {{{25}}^{\circ }}+\tan {{{25}}^{\circ }}\tan {{{20}}^{\circ }}}}{{\tan {{{25}}^{\circ }}\tan {{{20}}^{\circ }}}}} \right)\left( {\frac{{1-\tan {{{21}}^{\circ }}-\tan {{{24}}^{\circ }}+\tan {{{24}}^{\circ }}\tan {{{21}}^{\circ }}}}{{\tan {{{24}}^{\circ }}\tan {{{21}}^{\circ }}}}} \right)$ 

$\displaystyle \ \ \ \ \ \ \ =\left( {\frac{{2\tan {{{25}}^{\circ }}\tan {{{20}}^{\circ }}}}{{\tan {{{25}}^{\circ }}\tan {{{20}}^{\circ }}}}} \right)\left( {\frac{{2\tan {{{24}}^{\circ }}\tan {{{21}}^{\circ }}}}{{\tan {{{24}}^{\circ }}\tan {{{21}}^{\circ }}}}} \right)$

$\displaystyle \ \ \ \ \ \ \ =4$ 

$\displaystyle *Note$

$\displaystyle \tan {{45}^{\circ }}=\tan \left( {{{{25}}^{\circ }}+{{{20}}^{\circ }}} \right)=\frac{{\tan {{{25}}^{\circ }}+\tan {{{20}}^{\circ }}}}{{1-\tan {{{25}}^{\circ }}\tan {{{20}}^{\circ }}}}$ 

$\displaystyle \tan {{45}^{\circ }}=\tan \left( {{{{24}}^{\circ }}+{{{21}}^{\circ }}} \right)=\frac{{\tan {{{24}}^{\circ }}+\tan {{{21}}^{\circ }}}}{{1-\tan {{{24}}^{\circ }}\tan {{{21}}^{\circ }}}}$

$\displaystyle \tan {{45}^{\circ }}=1$ 

$\displaystyle \therefore \ \ \tan {{25}^{\circ }}\tan {{20}^{\circ }}=1-\tan {{25}^{\circ }}-\tan {{20}^{\circ }}\ \ and\ \ \tan {{24}^{\circ }}\tan {{21}^{\circ }}=1-\tan {{24}^{\circ }}-\tan {{21}^{\circ }}\ $ 

45-45 right triangle and Pythagoras theorem

ABCD is a square and E is the intersection point of the diagonals . If N is any point on AE , show that $\displaystyle A{{B}^{2}}-B{{N}^{2}}=AN.NC$ .

Solution

$\displaystyle \text{Let}\ AB=BC=x\ \ \text{and}\ \ NE=y$

$\displaystyle \Delta \ BCE\ \ \text{is}\ \ {{45}^{\circ }}\text{-}\ {{45}^{\circ }}\ rt\ \Delta .$ 

$\displaystyle \therefore \ BE=CE=\frac{x}{{\sqrt{2}}}$ 

$\displaystyle A{{B}^{2}}-B{{N}^{2}}={{x}^{2}}-\left( {B{{E}^{2}}+N{{E}^{2}}} \right)$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ={{x}^{2}}-\left( {{{{\left( {\frac{x}{{\sqrt{2}}}} \right)}}^{2}}+{{y}^{2}}} \right)$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ={{x}^{2}}-\frac{{{{x}^{2}}}}{2}-{{y}^{2}}$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{1}{2}{{x}^{2}}-{{y}^{2}}$ 

$\displaystyle AN.NC=\left( {AE-NE} \right)\left( {CE+NE} \right)$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ =\left( {\frac{x}{{\sqrt{2}}}-y} \right)\left( {\frac{x}{{\sqrt{2}}}+y} \right)$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ =\frac{1}{2}{{x}^{2}}-{{y}^{2}}$ 

$\displaystyle \therefore \ A{{B}^{2}}-B{{N}^{2}}=AN.NC$

Isosceles right triangle and cosines law

Isosceles triangle ABC has a right angle at C . Point P is inside triangle ABC such that
PA = 11 , PB = 7 and PC = 6 . Find the area of triangle ABC .

Solution

$ \displaystyle \text{By}\ \text{the}\ \text{law}\ \text{of}\ \text{cosines}\ ,$ 

$ \displaystyle \cos \theta =\frac{{B{{C}^{2}}+P{{C}^{2}}-P{{B}^{2}}}}{{2BC.PC}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{{{x}^{2}}+{{6}^{2}}-{{7}^{2}}}}{{2x\ .\ 6}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{{{x}^{2}}-13}}{{12x}}$ 

$ \displaystyle \cos ({{90}^{\circ }}-\theta )=\frac{{A{{C}^{2}}+P{{C}^{2}}-P{{A}^{2}}}}{{2AC.PC}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \sin \theta =\frac{{{{x}^{2}}+{{6}^{2}}-{{{11}}^{2}}}}{{2x\ .\ 6}}\ \ \ \left( {\because \cos ({{{90}}^{\circ }}-\theta )=\sin \theta } \right)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{{{x}^{2}}-85}}{{12x}}$

$ \displaystyle {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$ 

$\displaystyle {{\left( {\frac{{{{x}^{2}}-85}}{{12x}}} \right)}^{2}}+{{\left( {\frac{{{{x}^{2}}-13}}{{12x}}} \right)}^{2}}=1$ 

$\displaystyle \frac{{{{x}^{4}}-170{{x}^{2}}+7225}}{{144{{x}^{2}}}}\ +\ \frac{{{{x}^{4}}-26{{x}^{2}}+169}}{{144{{x}^{2}}}}=1$

$\displaystyle 2{{x}^{4}}-196{{x}^{2}}+7394=144{{x}^{2}}$

$\displaystyle 2{{x}^{4}}-340{{x}^{2}}+7394=0$ 

$\displaystyle \ \ {{x}^{4}}-170{{x}^{2}}+3697=0$ 

$\displaystyle \ {{x}^{4}}-170{{x}^{2}}+{{85}^{2}}={{85}^{2}}-3697$

$\displaystyle {{\left( {{{x}^{2}}-85} \right)}^{2}}=3528$

$\displaystyle \ \ \ \ {{x}^{2}}-85=42\sqrt{2}\ \ \ \ \left[ {\because \sin \theta >0} \right]$ 

$\displaystyle \ \ \ \ \ \ \ \ \ \ {{x}^{2}}=85+42\sqrt{2}$ 

$\displaystyle \therefore \ \alpha \ (\ \Delta \ ABC\ )=\frac{1}{2}{{x}^{2}}=\frac{{85+42\sqrt{2}}}{2}\ \ \text{sq}\ \text{units}$

Two externally tangent circle

Given : M is the midpoint of BC and as shown in figure .
Prove: BC = 2 AF

Solution

Given : M is the midpoint of BC and as shown in figure .
Prove: BC = 2 AF
$ \displaystyle \text{Proof}\ :\ \Delta \ BHA\sim \Delta \ BGC\ \ \left( {\because HA\parallel GC} \right)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \frac{{AB}}{{AH}}=\frac{{BC}}{{CG}}\ \ .......(1)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \text{In}\ \Delta \ BHA\ \ \text{and}\ \Delta \ FMA\ ,$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \angle \ BHA=\angle \ FMA={{90}^{\circ }}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \angle \ BAH=\angle \ FAM\ \ \left( {\because \text{opposite}\ \angle \text{s}} \right)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \Delta \ BHA\sim \Delta \ FMA\ \ \left( {AA\ \text{Cor}:} \right)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \frac{{AB}}{{AH}}=\frac{{AF}}{{AM}}\ \ .......(2)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \text{From}\ (1)\ \text{and}\ (2),$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \frac{{BC}}{{CG}}=\frac{{AF}}{{AM}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \frac{{BC}}{{R-r}}=\frac{{AF}}{{\frac{1}{2}(R+r)-r}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \frac{{BC}}{{R-r}}=\frac{{2AF}}{{R-r}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \therefore \ BC=2AF$


 

Basic trigonometry formula and double angle formula

If $ \displaystyle 0<\theta <\frac{\pi }{4}$ is such that $ \displaystyle \operatorname{cosec}\theta -\sec \theta =\frac{{\sqrt{{13}}}}{6}$ , then find $ \displaystyle \left( {\cot \theta -\tan \theta } \right)$ .

Solution

$ \displaystyle \operatorname{cosec}\theta -\sec \theta =\frac{{\sqrt{{13}}}}{6}\ ,\ \ \ 0<\theta <\frac{\pi }{4}$

$ \displaystyle \ \ \frac{1}{{\sin \theta }}-\frac{1}{{\cos \theta }}=\frac{{\sqrt{{13}}}}{6}$

$ \displaystyle \ \ \ \frac{{\cos \theta -\sin \theta }}{{\sin \theta \cos \theta }}=\frac{{\sqrt{{13}}}}{6}$

$ \displaystyle \frac{{{{{\cos }}^{2}}\theta -2\sin \theta \cos \theta +{{{\sin }}^{2}}\theta }}{{{{{\sin }}^{2}}\theta {{{\cos }}^{2}}\theta }}=\frac{{13}}{{36}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{1-\sin 2\theta }}{{\frac{1}{4}{{{\sin }}^{2}}2\theta }}=\frac{{13}}{{36}}$ 

$ \displaystyle \ 13{{\sin }^{2}}2\theta +144\sin 2\theta -144=0$ 

$\displaystyle \ (13\sin 2\theta -12)(\sin 2\theta +12)=0$

$ \displaystyle 13\sin 2\theta -12=0\ \ (or)\ \ \sin 2\theta +12=0$

$ \displaystyle \sin 2\theta =\frac{{12}}{{13}}\ \ \ (or)\ \ \sin 2\theta =-12\ (reject)$

$ \displaystyle \therefore \ \sin 2\theta =\frac{{12}}{{13}}\ $

$ \displaystyle \cot \theta -\tan \theta =\frac{{\cos \theta }}{{\sin \theta }}-\frac{{\sin \theta }}{{\cos \theta }}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{{{{\cos }}^{2}}\theta -{{{\sin }}^{2}}\theta }}{{\sin \theta \cos \theta }}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{2\cos 2\theta }}{{\sin 2\theta }}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =2\cot 2\theta $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =2\times \frac{5}{{12}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{5}{6}\ \ \ $

The distance between vertex and orthocentre of a triangle

In $ \displaystyle \Delta \ ABC,\ \angle A={{60}^{\circ }},\ BC=5$ ,then find the distance of the vertex A from the orthocentre of  $ \displaystyle \Delta \ ABC\ $ .

Solution

$ \displaystyle BF=5\sin \theta \ \ \ ,\ \ CF=5\cos \theta $ 

$ \displaystyle GF=5\sin \theta \tan {{30}^{\circ }}$

$ \displaystyle \ \ \ \ \ \ =\frac{5}{{\sqrt{3}}}\sin \theta $ 

$ \displaystyle \text{By}\ \text{the}\ \text{law}\ \text{of}\ \text{sines}\ ,$ 

$ \displaystyle \frac{{AG}}{{\sin {{{30}}^{\circ }}}}=\frac{{CG}}{{\sin \ ({{{60}}^{\circ }}-\theta )}}$ 

$ \displaystyle \ \ \ 2AG=\frac{{CF-GF}}{{\sin {{{60}}^{\circ }}\cos \theta -\cos {{{60}}^{\circ }}\sin \theta }}$

$ \displaystyle \ \ \ 2AG=\frac{{5\cos \theta -\frac{5}{{\sqrt{3}}}\sin \theta }}{{\frac{{\sqrt{3}}}{2}\cos \theta -\frac{1}{2}\sin \theta }}$

$ \displaystyle \ \ \ \ \ AG=\frac{{\frac{5}{{\sqrt{3}}}(\sqrt{3}\cos \theta -\sin \theta )}}{{\sqrt{3}\cos \theta -\sin \theta }}$

$ \displaystyle \ \ \therefore \ AG=\frac{5}{{\sqrt{3}}}$

Change of base

Suppose that  $ \displaystyle a,b\ \text{and}\ c$ are real numbers greater than 1 .Find the value of $ \displaystyle \frac{1}{{1+{{{\log }}_{{{{a}^{2}}b}}}\left( {\frac{c}{a}} \right)}}+\frac{1}{{1+{{{\log }}_{{{{b}^{2}}c}}}\left( {\frac{a}{b}} \right)}}+\frac{1}{{1+{{{\log }}_{{{{c}^{2}}a}}}\left( {\frac{b}{c}} \right)}}$ .

Solution

$ \displaystyle \frac{1}{{1+{{{\log }}_{{{{a}^{2}}b}}}\left( {\frac{c}{a}} \right)}}+\frac{1}{{1+{{{\log }}_{{{{b}^{2}}c}}}\left( {\frac{a}{b}} \right)}}+\frac{1}{{1+{{{\log }}_{{{{c}^{2}}a}}}\left( {\frac{b}{c}} \right)}}$ 

$ \displaystyle =\frac{1}{{{{{\log }}_{{{{a}^{2}}b}}}{{a}^{2}}b+{{{\log }}_{{{{a}^{2}}b}}}\left( {\frac{c}{a}} \right)}}+\frac{1}{{{{{\log }}_{{{{b}^{2}}c}}}{{b}^{2}}c+{{{\log }}_{{{{b}^{2}}c}}}\left( {\frac{a}{b}} \right)}}+\frac{1}{{{{{\log }}_{{{{c}^{2}}a}}}{{c}^{2}}a+{{{\log }}_{{{{c}^{2}}a}}}\left( {\frac{b}{c}} \right)}}$ 

$ \displaystyle =\frac{1}{{{{{\log }}_{{{{a}^{2}}b}}}abc}}+\frac{1}{{{{{\log }}_{{{{b}^{2}}c}}}abc}}+\frac{1}{{{{{\log }}_{{{{c}^{2}}a}}}abc}}$ 

$ \displaystyle ={{\log }_{{abc}}}{{a}^{2}}b+{{\log }_{{abc}}}{{b}^{2}}c+{{\log }_{{abc}}}{{c}^{2}}a$

$ \displaystyle ={{\log }_{{abc}}}{{(abc)}^{3}}$ 

$ \displaystyle =3$

Solving problem with Double Angle Formula

$ \displaystyle \text{Prove}\ \text{that}\ \ \ \frac{1}{2}\sqrt{{4{{{\sin }}^{2}}{{{36}}^{\circ }}-1}}=\cos {{72}^{\circ }}.$

$ \displaystyle \text{Solution}$

$ \displaystyle \ \ \ \cos {{72}^{\circ }}=2{{\cos }^{2}}{{36}^{\circ }}-1\ \ \ ........(1)$

$ \displaystyle \ \ \ \cos {{144}^{\circ }}=2{{\cos }^{2}}{{72}^{\circ }}-1$ 

$ \displaystyle \ \ \ -\cos {{36}^{\circ }}=2{{\cos }^{2}}{{72}^{\circ }}-1$

$ \displaystyle \ \ \ \ \ \cos {{36}^{\circ }}=1-2{{\cos }^{2}}{{72}^{\circ }}\ \ .......(2)$

$ \displaystyle (1)+(2)\Rightarrow \ \ \ \cos {{72}^{\circ }}+\cos {{36}^{\circ }}=2\ (\ {{\cos }^{2}}{{36}^{\circ }}-{{\cos }^{2}}{{72}^{\circ }})$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cos {{36}^{\circ }}-\cos {{72}^{\circ }}=\frac{1}{2}$

$ \displaystyle (2)-(1)\Rightarrow \ \ \ \cos {{36}^{\circ }}-\cos {{72}^{\circ }}=2-2\ (\ {{\cos }^{2}}{{36}^{\circ }}+{{\cos }^{2}}{{72}^{\circ }})$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{2}=2-2\ (\ {{\cos }^{2}}{{36}^{\circ }}+{{\cos }^{2}}{{72}^{\circ }})$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2\ (\ {{\cos }^{2}}{{36}^{\circ }}+{{\cos }^{2}}{{72}^{\circ }})=\frac{3}{2}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\cos }^{2}}{{36}^{\circ }}+{{\cos }^{2}}{{72}^{\circ }}=\frac{3}{4}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 1-{{\sin }^{2}}{{36}^{\circ }}+{{\cos }^{2}}{{72}^{\circ }}=\frac{3}{4}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\sin }^{2}}{{36}^{\circ }}-{{\cos }^{2}}{{72}^{\circ }}=\frac{1}{4}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 4{{\sin }^{2}}{{36}^{\circ }}-4{{\cos }^{2}}{{72}^{\circ }}=1$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 4{{\sin }^{2}}{{36}^{\circ }}-1=4{{\cos }^{2}}{{72}^{\circ }}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sqrt{{4{{{\sin }}^{2}}{{{36}}^{\circ }}-1}}=2\cos {{72}^{\circ }}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore \ \ \frac{1}{2}\sqrt{{4{{{\sin }}^{2}}{{{36}}^{\circ }}-1}}=\cos {{72}^{\circ }}$

Positive real numbers and their equations

Given : $ \displaystyle a,b$ are positive real numbers such that $ \displaystyle a\sqrt{a}+b\sqrt{b}=183$ and $ \displaystyle a\sqrt{b}+b\sqrt{a}=182$ .
Find : $ \displaystyle \frac{9}{5}\ (\ a+b\ )$

Solution

$ \displaystyle a\sqrt{a}+b\sqrt{b}=183$

$ \displaystyle {{(\ \sqrt{a}\ )}^{3}}+{{(\ \sqrt{b}\ )}^{3}}=183$

$ \displaystyle {{(\ \sqrt{a}+\sqrt{b}\ )}^{3}}-3\sqrt{{ab}}(\ \sqrt{a}+\sqrt{b}\ )=183\ ........(1)$

$ \displaystyle a\sqrt{b}+b\sqrt{a}=182$ 

$ \displaystyle \sqrt{{ab}}\ (\ \sqrt{a}+\sqrt{b}\ )=182\ \ .............(2)$ 

$ \displaystyle \text{From}\ (1)\ \text{and}\ (2),$

$ \displaystyle {{(\ \sqrt{a}+\sqrt{b}\ )}^{3}}-546=183$

$ \displaystyle \ \ \ \ \ \ \ \ {{(\ \sqrt{a}+\sqrt{b}\ )}^{3}}=729$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \sqrt{a}+\sqrt{b}=9\ \ \ .............(3)$

$ \displaystyle \text{From}\ (2)\ \text{and}\ (3),$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \sqrt{{ab}}=\frac{{182}}{9}$

$ \displaystyle {{(\ \sqrt{a}+\sqrt{b}\ )}^{2}}=81\ \ \ \ \left[ {By\ (3)} \right]$

$ \displaystyle a+b+2\sqrt{{ab}}=81$

$ \displaystyle \ \ a+b+\frac{{364}}{9}=81$

$ \displaystyle \ a+b=\frac{{365}}{9}=73\times \frac{5}{9}$

$ \displaystyle \therefore \ \ \frac{9}{5}\ (\ a+b\ )=73$

 

Solving problem with basic trigonometry formula and double angle formula

$ \displaystyle \text{Prove}\ \text{that}\ \operatorname{cosec}\frac{{{{{180}}^{\circ }}}}{7}=\ \operatorname{cosec}\frac{{{{{360}}^{\circ }}}}{7}+\ \operatorname{cosec}\frac{{{{{540}}^{\circ }}}}{7}.$


Solution

$ \displaystyle \ \operatorname{cosec}\frac{{{{{360}}^{\circ }}}}{7}+\ \operatorname{cosec}\frac{{{{{540}}^{\circ }}}}{7}=\frac{1}{{\sin \frac{{2\pi }}{7}}}+\frac{1}{{\sin \frac{{3\pi }}{7}}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\sin \frac{{3\pi }}{7}+\sin \frac{{2\pi }}{7}}}{{\sin \frac{{2\pi }}{7}\sin \frac{{3\pi }}{7}}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{2\sin \frac{{5\pi }}{{14}}\cos \frac{\pi }{{14}}}}{{2\sin \frac{\pi }{7}\cos \frac{\pi }{7}\cos \frac{\pi }{{14}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\cos \frac{\pi }{7}}}{{\sin \frac{\pi }{7}\cos \frac{\pi }{7}}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ \operatorname{cosec}\frac{\pi }{7}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ \operatorname{cosec}\frac{{{{{180}}^{\circ }}}}{7}$

Solving problem with Sines Law and Compound Angle Formula

X  is any point on the side BC of a triangle ABC . If the $ \displaystyle \angle AXC=\theta \ and\ \frac{{BX}}{{XC}}=\frac{m}{n}$ , show that $ \displaystyle (m+n)\cos \theta =n\cot B-m\cot C$ .

Solution

$ \displaystyle \text{Proof}:\ \ \text{By}\ \text{the}\ \text{law}\ \text{of}\ \text{sines}\ ,$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \frac{{BX}}{{\sin \beta }}=\frac{{AB}}{{\sin ({{{180}}^{\circ }}-\theta )}}=\frac{{AB}}{{\sin \theta }}\ \ .....(1)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \frac{{XC}}{{\sin \alpha }}=\frac{{AC}}{{\sin \theta }}\ \ \ ..........(2)$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \frac{{AB}}{{\sin C}}=\frac{{AC}}{{\sin B}}\ \ \ ..........(3)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ (1)\div (2)\Rightarrow \ \ \ \frac{{BX\sin \alpha }}{{XC\sin \beta }}=\frac{{AB}}{{AC}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{m\sin \alpha }}{{n\sin \beta }}=\frac{{\sin C}}{{\sin B}}\ \ \ \ [\text{By}\ (3)]$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{m\sin ({{{180}}^{\circ }}-(\theta +C))}}{{n\sin (\theta -B)}}=\frac{{\sin C}}{{\sin B}}\ $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{m\sin (\theta +C)}}{{n\sin (\theta -B)}}=\frac{{\sin C}}{{\sin B}}\ $ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \frac{{m(\sin \theta \cos C+\cos \theta \sin C)}}{{\sin C}}=\frac{{n(\sin \theta \cos B-\cos \theta \sin B)}}{{\sin B}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ m\sin \theta \cot C+m\cos \theta =n\sin \theta \cot B-n\cos \theta $ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (m+n)\cos \theta \ =\sin \theta \ (\ n\cot B-m\cot C\ )$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore \ \ \ \ (m+n)\cot \theta \ =\ n\cot B-m\cot C$

Solving problem with Sines Law and Cosine Law

In triangle ABC, the lengths of the three sides of the triangle are $ \displaystyle a\ cm,b\ cm\ and\ c\ cm$ . It is given that $ \displaystyle \frac{{{{a}^{2}}+{{b}^{2}}}}{{{{c}^{2}}}}=2016$. Find the value of $ \displaystyle \frac{{\cot C}}{{\cot A+\cot B}}$ .

Solution

$ \displaystyle \frac{{{{a}^{2}}+{{b}^{2}}}}{{{{c}^{2}}}}=2016$ 

$ \displaystyle {{a}^{2}}+{{b}^{2}}=2016\ {{c}^{2}}$ 

$ \displaystyle {{a}^{2}}+{{b}^{2}}-{{c}^{2}}=2015\ {{c}^{2}}$ 

$ \displaystyle 2ab\cos C=2015\ {{c}^{2}}\ \ (\because \ \ \cos C=\frac{{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}}{{2ab}})$

$ \displaystyle \ \ \ \ \ \ \cos C=\frac{{2015\ {{c}^{2}}}}{{2ab}}$ 

$ \displaystyle \frac{{\cot C}}{{\cot A+\cot B}}=\frac{{\frac{{\cos C}}{{\sin C}}}}{{\frac{{\cos A}}{{\sin A}}+\frac{{\cos B}}{{\sin B}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\frac{{\cos C}}{{\sin C}}}}{{\frac{{\sin B\cos A+\cos B\sin A}}{{\sin A\sin B}}}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\cos C}}{{\sin C}}\times \frac{{\sin A\sin B}}{{\sin (B+A)}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\cos C}}{{\sin C}}\times \frac{{\sin A\sin B}}{{\sin ({{{180}}^{\circ }}-C)}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\cos C}}{{\sin C}}\times \frac{{\sin A\sin B}}{{\sin C}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\cos C\times \frac{{\sin A}}{{\sin C}}\times \frac{{\sin B}}{{\sin C}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{2015\ {{c}^{2}}}}{{2ab}}\times \frac{a}{c}\times \frac{b}{c}\ \ (\because \ \frac{a}{{\sin A}}=\frac{b}{{\sin B}}=\frac{c}{{\sin C}})$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{2015}}{2}$