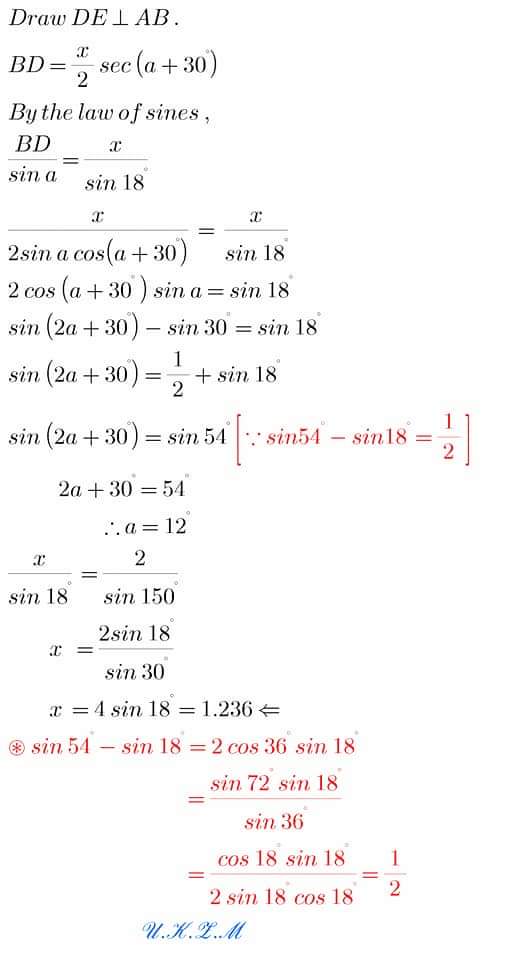The largest right circular cone

Find the volume of the largest right circular cone that can be inscribed in a sphere of radius 3 .

Solution

$ \displaystyle \text{Volume}\ \text{of}\ \text{right}\ \text{circular}\ \text{cone}\ =V=\frac{1}{3}\pi {{x}^{2}}(3+y)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{1}{3}\pi {{x}^{2}}(\ 3+\sqrt{{9-{{x}^{2}}}}\ )$

$ \displaystyle \frac{{dV}}{{dx}}=\frac{1}{3}\pi \left[ {{{x}^{2}}.\frac{1}{2}{{{(9-{{x}^{2}})}}^{{-\frac{1}{2}}}}(-2x)+(\ 3+\sqrt{{9-{{x}^{2}}}}\ ).2x} \right]$

$ \displaystyle \ \ \ \ \ =\frac{1}{3}\pi \left[ {-\frac{{{{x}^{3}}}}{{\sqrt{{9-{{x}^{2}}}}}}+6x+2x\sqrt{{9-{{x}^{2}}}}} \right]$ 

$ \displaystyle \ \ \ \ \ =\frac{1}{3}\pi \left[ {6x+\frac{{-{{x}^{3}}+18x-2{{x}^{3}}}}{{\sqrt{{9-{{x}^{2}}}}}}} \right]$

$ \displaystyle \ \ \ \ \ =\frac{1}{3}\pi \left[ {6x+\frac{{18x-3{{x}^{3}}}}{{\sqrt{{9-{{x}^{2}}}}}}} \right]$

$ \displaystyle \ \ \ \ \ =\pi \left[ {2x+\frac{{6x-{{x}^{3}}}}{{\sqrt{{9-{{x}^{2}}}}}}} \right]$ 

$ \displaystyle \text{For}\ \text{stationary}\ \text{value}\ ,\ \frac{{dV}}{{dx}}=0$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \pi \left[ {2x+\frac{{6x-{{x}^{3}}}}{{\sqrt{{9-{{x}^{2}}}}}}} \right]=0$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{6x-{{x}^{3}}}}{{\sqrt{{9-{{x}^{2}}}}}}=-2x$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 6-{{x}^{2}}=-2\sqrt{{9-{{x}^{2}}}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 36-12{{x}^{2}}+{{x}^{4}}=36-4{{x}^{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}^{4}}-8{{x}^{2}}=0$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}^{2}}=8$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x=\sqrt{8}$

$ \displaystyle \frac{{{{d}^{2}}V}}{{d{{x}^{2}}}}=\pi \left[ {2+\frac{{\sqrt{{9-{{x}^{2}}}}(6-3{{x}^{2}})-(6x-{{x}^{3}})\frac{1}{2}{{{(9-{{x}^{2}})}}^{{-\frac{1}{2}}}}(-2x)}}{{9-{{x}^{2}}}}} \right]$

$ \displaystyle \ \ \ \ \ \ =\pi \left[ {2+\frac{{(9-{{x}^{2}})(6-3{{x}^{2}})+{{x}^{2}}(6-{{x}^{2}})}}{{(9-{{x}^{2}})\sqrt{{9-{{x}^{2}}}}}}} \right]$ 

$ \displaystyle \text{when}\ x=\sqrt{8}\ ,\ \frac{{{{d}^{2}}V}}{{d{{x}^{2}}}}=\pi (2-18-16)=-32\pi <0\ $

$ \displaystyle V\ \text{is}\ \text{maximum}\ \text{value}\ \text{when}\ x=\sqrt{8}\ .$ 

$ \displaystyle \text{The}\ \text{volume}\ \text{of}\ \text{the}\ \text{largest}\ \text{right}\ \text{circular}\ \text{cone}\ =V=\frac{1}{3}\times \frac{{22}}{7}\times 32$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{704}}{{21}}\ \text{cube}\ \text{units}$

Calculus : Maximum and Minimum

Find the dimensions of the right circular cylinder of largest volume that can be inscribed in a sphere of radius  R .

Solution

$ \displaystyle \text{Let}\ \text{the}\ \text{volume}\ \text{of}\ \text{cylinder}\ =\ V=\pi {{r}^{2}}h$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ {{r}^{2}}+{{\left( {\frac{h}{2}} \right)}^{2}}={{R}^{2}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ {{r}^{2}}={{R}^{2}}-\frac{{{{h}^{2}}}}{4}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ V=\pi \left( {{{R}^{2}}-\frac{{{{h}^{2}}}}{4}} \right)h$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ =\pi \left( {{{R}^{2}}h-\frac{1}{4}{{h}^{3}}} \right)$

$ \displaystyle \ \ \ \ \ \ \ \frac{{dV}}{{dh}}=\pi \left( {{{R}^{2}}-\frac{3}{4}{{h}^{2}}} \right)$ 

$ \displaystyle \text{For}\ \text{stationary}\ \text{value}\ ,\ \frac{{dV}}{{dh}}=0$ 

$ \displaystyle \ \ \ \ \ \ \ \pi \left( {{{R}^{2}}-\frac{3}{4}{{h}^{2}}} \right)=0$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ {{R}^{2}}-\frac{3}{4}{{h}^{2}}=0$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{h}^{2}}=\frac{{4{{R}^{2}}}}{3}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ h=\frac{{2R}}{{\sqrt{3}}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \frac{{{{d}^{2}}V}}{{d{{h}^{2}}}}=-\frac{3}{2}\pi h$ 

$ \displaystyle \text{When}\ \ h=\frac{{2R}}{{\sqrt{3}}}\ \ ,\ \ \ \ \frac{{{{d}^{2}}V}}{{d{{h}^{2}}}}=-\sqrt{3}\ \pi R\ <\ 0$ 

$ \displaystyle V\ \text{is}\ \text{maximum}\ \text{value}\ \text{when}\ \ h=\frac{{2R}}{{\sqrt{3}}}\ $ 

$ \displaystyle \ \ \ \ \ \ \ {{r}^{2}}={{R}^{2}}-\frac{{{{R}^{2}}}}{3}=\frac{{2{{R}^{2}}}}{3}$ 

$ \displaystyle \therefore \ \ \ r\ =\sqrt{{\frac{2}{3}}}\ R$

The sum of the series

Find the value of sum of

$ \displaystyle \frac{1}{{11}}+\frac{1}{{11+22}}+\frac{1}{{11+22+33}}+...+\frac{1}{{11+22+33+...+2013}}$ .

Solution

$ \displaystyle \frac{1}{{11}}+\frac{1}{{11+22}}+\frac{1}{{11+22+33}}+...+\frac{1}{{11+22+33+...+2013}}$

$ \displaystyle =\frac{1}{{11}}\ \left[ {1+\frac{1}{{1+2}}+\frac{1}{{1+2+3}}+...+\frac{1}{{1+2+3+...+183}}} \right]$ 

$ \displaystyle =\frac{1}{{11}}\ \left[ {1+\frac{1}{3}+\frac{1}{6}+...+\frac{1}{{\frac{{183}}{2}(1+183)}}} \right]$ 

$ \displaystyle =\frac{1}{{11}}\left[ {1+\frac{1}{3}+\frac{1}{6}+...+\frac{2}{{183\times 184}}} \right]$ 

$ \displaystyle =\frac{2}{{11}}\left[ {\frac{1}{2}+\frac{1}{6}+\frac{1}{{12}}+...+\frac{1}{{183\times 184}}} \right]$

$ \displaystyle =\frac{2}{{11}}\left[ {\frac{1}{{1\times 2}}+\frac{1}{{2\times 3}}+\frac{1}{{3\times 4}}+...+\frac{1}{{183\times 184}}} \right]$ 

$ \displaystyle =\frac{2}{{11}}\ \left[ {\left( {\frac{1}{1}-\frac{1}{2}} \right)+\left( {\frac{1}{2}-\frac{1}{3}} \right)+\left( {\frac{1}{3}-\frac{1}{4}} \right)+...+\left( {\frac{1}{{183}}-\frac{1}{{184}}} \right)} \right]$ 

$ \displaystyle =\frac{2}{{11}}\left( {1-\frac{1}{{184}}} \right)$ 

$ \displaystyle =\frac{2}{{11}}\times \frac{{183}}{{184}}$ 

$ \displaystyle =\frac{{183}}{{1012}}$

Angle bisector theorem

Given : ABCD is a square , CF bisects $ \displaystyle \angle ACD$ , BPQ perpendicular CF .
Prove : DQ = 2PE .

$ \displaystyle \text{Proof}\ :\ \ \theta =\beta =\alpha =\gamma ={{22.5}^{\circ }}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ In\ \Delta CQG\ \ and\ \ \Delta CPG\ ,$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \theta =\beta $ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \angle CGQ=\angle CGP={{90}^{\circ }}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ CG=CG\ \ (\ \text{common}\ \text{side}\ )$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \Delta CQG\cong \Delta CPG\ (\ A.S.A\ )$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore \ CQ=CP$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \frac{{CQ}}{{DQ}}=\frac{{BC}}{{BD}}\ \ (\ \because \ \text{Angle}\ \text{bisector}\ \text{theorem}\ )$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \frac{{CQ}}{{DQ}}=\frac{1}{{\sqrt{2}}}\ .........(1)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \frac{{PE}}{{CP}}=\frac{{BE}}{{BC}}\ \ (\ \because \ \text{Angle}\ \text{bisector}\ \text{theorem}\ )$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \frac{{PE}}{{CP}}=\frac{1}{{\sqrt{2}}}\ .........(2)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ (1)\ \times \ (2)\Rightarrow \ \ \frac{{CQ}}{{DQ}}\ \times \ \frac{{PE}}{{CP}}=\frac{1}{2}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{PE}}{{DQ}}=\frac{1}{2}\ (\ \because \ CQ=CP\ )$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore \ \ \ DQ\ =2PE$

Area: Trapezium

Parallel sides of a trapezium are equal to a and b . Find the length of the line segment which is parallel to them and divides the area of the trapezium into two equal parts.
( i.e Find x in terms of a and b .)

Solution

Draw AD and BC produced meet at G .

$ \displaystyle \text{Let}\ \alpha (\Delta GDC)=P\ ,\ \alpha (DEFG)=Q\ \ ,\ \alpha (ABFE)=R$ 

$ \displaystyle \Delta GDC\sim \Delta GEF\sim \Delta GAB\ \ (\because DC\parallel EF\parallel AB)$ 

$ \displaystyle \frac{P}{{P+Q}}=\frac{{{{b}^{2}}}}{{{{x}^{2}}}}$ 

$ \displaystyle \frac{P}{Q}=\frac{{{{b}^{2}}}}{{{{x}^{2}}-{{b}^{2}}}}\ ........(1)$

$ \displaystyle \frac{P}{{P+Q+R}}=\frac{{{{b}^{2}}}}{{{{a}^{2}}}}$ 

$ \displaystyle \frac{P}{{Q+R}}=\frac{{{{b}^{2}}}}{{{{a}^{2}}-{{b}^{2}}}}$

$ \displaystyle \frac{P}{{2Q}}=\frac{{{{b}^{2}}}}{{{{a}^{2}}-{{b}^{2}}}}\ \ (\because \ Q=R)$ 

$ \displaystyle \frac{P}{Q}=\frac{{2{{b}^{2}}}}{{{{a}^{2}}-{{b}^{2}}}}\ ........(2)$

$ \displaystyle \text{From}\ (1)\ \text{and}\ (2)\ ,\ \frac{{{{b}^{2}}}}{{{{x}^{2}}-{{b}^{2}}}}\ =\frac{{2{{b}^{2}}}}{{{{a}^{2}}-{{b}^{2}}}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2{{x}^{2}}-2{{b}^{2}}={{a}^{2}}-{{b}^{2}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2{{x}^{2}}={{a}^{2}}+{{b}^{2}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore \ \ \ x=\sqrt{{\frac{{{{a}^{2}}+{{b}^{2}}}}{2}}}$

Fermat point

$ \displaystyle \Delta ABC$ is a $ \displaystyle {{30}^{\circ }}-{{60}^{\circ }}$ right triangle with $ \displaystyle \angle A={{30}^{\circ }}\ ,\ \angle B={{60}^{\circ }}$. If P is a Fermat point of $ \displaystyle \Delta ABC$ , prove that AP , BP , CP are in a G.P.

Solution

$ \displaystyle \text{In}\ \Delta FCB\ \text{and}\ \Delta ACD\ ,$ 

$ \displaystyle \ \ \ \ \ FC\ =\ AC$ 

$ \displaystyle \ \ \ \ \ CB=CD$ 

$ \displaystyle \angle FCB=\angle ACD$ 

$ \displaystyle \Delta FCB\cong \Delta ACD\ \ (S.A.S)$ 

$\displaystyle \angle FBC=\angle ADC=\beta $ 

$ \displaystyle \therefore \ CDBP\ \text{is}\ \text{cyclic}\ .$

$ \displaystyle \angle PCB=\angle PDB=\theta $ 

$ \displaystyle AB\parallel \ CD\ \ (\because \ \angle BCD=\angle ABC)$

$ \displaystyle \therefore \ \angle ADC=\angle BAD\ \ (\because \text{alternate}\ \angle \text{s})$ 

$ \displaystyle \text{By}\ \text{the}\ \text{law}\ \text{of}\ \text{sines}\ ,$ 

$ \displaystyle \ \ \ \ \ \frac{{BP}}{{\sin \beta }}=\frac{{AP}}{{\sin \theta }}$ 

$ \displaystyle \ \ \ \ \ \ \ \frac{{BP}}{{AP}}=\frac{{\sin \beta }}{{\sin \theta }}\ \ \ \ \ \ \ ........(1)$ 

$ \displaystyle \ \ \ \ \ \ \frac{{CP}}{{\sin \beta }}=\frac{{BP}}{{\sin \theta }}$

$ \displaystyle \ \ \ \ \ \ \ \frac{{CP}}{{BP}}=\frac{{\sin \beta }}{{\sin \theta }}\ \ \ \ \ \ \ ........(2)$ 

$ \displaystyle \text{From}\,(1)\ \ \text{and}\ (2)\ ,\ \ \frac{{BP}}{{AP}}=\ \frac{{CP}}{{BP}}$ 

$ \displaystyle \therefore \ AP,BP,CP\ \text{are}\ \text{in}\ \text{a}\ G.P.\ $

Area of shaded region

In the figure , a square ABCD and a sector OAB of a circle centre O , radius r . Show that the area of square ABCD is $ \displaystyle 2{{r}^{2}}(1-\cos \theta )$ and then find the shaded area R , when $ \displaystyle \theta =\frac{\pi }{3}$ .

Solution

$ \displaystyle \text{Draw}\ \ OE\bot AB\ .$  

$ \displaystyle AE=r\sin \frac{\theta }{2}\ \ \ ,\ \ \ OE=r\cos \frac{\theta }{2}$ 

$ \displaystyle AB=2AE=2r\sin \frac{\theta }{2}\ $

$ \displaystyle \alpha (ABCD)={{(2r\sin \frac{\theta }{2}\ )}^{2}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =4{{r}^{2}}{{\sin }^{2}}\frac{\theta }{2}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =2{{r}^{2}}\ .\ 2{{\sin }^{2}}\frac{\theta }{2}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =2{{r}^{2}}\ (1-\cos \theta )\ \ \ \ [\because \cos 2\theta =1-2{{\sin }^{2}}\theta ]$

$ \displaystyle \text{The}\ \text{shaded}\ \text{area}\ R\ =\alpha (ABCD)+\alpha (\Delta OAB)-\text{Area}\ \text{of}\ \text{sector}\ OAB$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =2{{r}^{2}}\ (1-\cos \theta )+\frac{1}{2}(2r\sin \frac{\theta }{2}\ )(r\cos \frac{\theta }{2})-\frac{1}{2}{{r}^{2}}\theta $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =2{{r}^{2}}\ (1-\cos \theta )+\frac{1}{2}{{r}^{2}}\sin \theta -\frac{1}{2}{{r}^{2}}\theta $

$ \displaystyle \text{When}\ \theta =\frac{\pi }{3}\ ,$

$ \displaystyle R=2{{r}^{2}}(1-\frac{1}{2})+\frac{1}{2}{{r}^{2}}(\frac{{\sqrt{3}}}{2})-\frac{1}{2}{{r}^{2}}(\frac{\pi }{3})$

$ \displaystyle \ \ \ =(1+\frac{{\sqrt{3}}}{4}-\frac{\pi }{6})\ {{r}^{2}}\ \text{sq}\ \text{units}$

Descartes' Circle Theorem

$ \displaystyle \alpha +\beta +\gamma =2\pi $

$ \displaystyle \cos 2\alpha +\cos 2\beta +\cos 2\gamma $

$ \displaystyle =2{{\cos }^{2}}\alpha -1+2{{\cos }^{2}}\beta -1+2{{\cos }^{2}}\gamma -1$

$ \displaystyle =2({{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma )-3\ \ \ .............(1)$

$ \displaystyle \cos 2\alpha +\cos 2\beta +\cos 2\gamma $

$ \displaystyle =2\cos (\alpha +\beta )\cos (\alpha -\beta )+2{{\cos }^{2}}\gamma -1$

$ \displaystyle =2\cos (2\pi -\gamma )\cos (\alpha -\beta )+2{{\cos }^{2}}\gamma -1$

$ \displaystyle =2\cos \gamma \cos (\alpha -\beta )+2{{\cos }^{2}}\gamma -1$

$ \displaystyle =2\cos \gamma \ [\ \cos (\alpha -\beta )+\cos \gamma \ ]-1\ \ $

$ \displaystyle =2\cos \gamma \ [\ \cos (\alpha -\beta )+\cos (\alpha +\beta )\ ]-1\ $

$ \displaystyle =4\cos \alpha \cos \beta \cos \gamma -1\ \ \ \ \ .........................(2)$

$ \displaystyle \text{From}\ (1)\ \text{and}\ \ (2)\ ,$

$ \displaystyle 2({{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma )-3=4\cos \alpha \cos \beta \cos \gamma -1\ $

$ \displaystyle \therefore \ {{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1+2\cos \alpha \cos \beta \cos \gamma $

$ \displaystyle Let\ \angle AOB=\gamma \ ,\ \angle BOC=\alpha \ \ ,\ \angle AOC=\beta $

$ \displaystyle \text{By}\ \text{the}\ \text{law}\ \text{of}\ \text{cosines}\ ,$

$ \displaystyle \cos \gamma =\frac{{O{{A}^{2}}+O{{B}^{2}}-A{{B}^{2}}}}{{2\ OA\ .\ OB}}$

$ \displaystyle \ \ \ \ \ \ \ =\frac{{{{{({{r}_{4}}+{{r}_{1}})}}^{2}}+{{{({{r}_{4}}+{{r}_{2}})}}^{2}}-{{{({{r}_{1}}+{{r}_{2}})}}^{2}}}}{{2\ ({{r}_{4}}+{{r}_{1}})\ ({{r}_{4}}+{{r}_{2}})}}$

$ \displaystyle \ \ \ \ \ \ \ =\frac{{2{{r}_{4}}^{2}+2{{r}_{4}}({{r}_{1}}+{{r}_{2}})-2{{r}_{1}}{{r}_{2}}}}{{2\ ({{r}_{4}}+{{r}_{1}})\ ({{r}_{4}}+{{r}_{2}})}}$

$ \displaystyle \ \ \ \ \ \ \ =1-\frac{{2{{r}_{1}}{{r}_{2}}}}{{({{r}_{4}}+{{r}_{1}})\ ({{r}_{4}}+{{r}_{2}})}}$

$ \displaystyle \cos \gamma =1-\frac{{2{{k}_{4}}^{2}}}{{({{k}_{4}}+{{k}_{1}})({{k}_{4}}+{{k}_{2}})}}=1-{{\lambda }_{3}}$

$ \displaystyle \text{Similarly}\ \text{,}\ \text{we}\ \text{have}$

$ \displaystyle \cos \beta =1-\frac{{2{{k}_{4}}^{2}}}{{({{k}_{4}}+{{k}_{1}})({{k}_{4}}+{{k}_{3}})}}=1-{{\lambda }_{2}}$

$ \displaystyle \cos \alpha =1-\frac{{2{{k}_{4}}^{2}}}{{({{k}_{4}}+{{k}_{2}})({{k}_{4}}+{{k}_{3}})}}=1-{{\lambda }_{1}}$

$ \displaystyle {{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +{{\cos }^{2}}\gamma =1+2\cos \alpha \cos \beta \cos \gamma $

$ \displaystyle {{(1-{{\lambda }_{1}})}^{2}}+{{(1-{{\lambda }_{2}})}^{2}}+{{(1-{{\lambda }_{3}})}^{2}}=1+2(1-{{\lambda }_{1}})(1-{{\lambda }_{2}})(1-{{\lambda }_{3}})$

$ \displaystyle \text{Simplifying}\ \text{,}\ \text{we}\ \text{get}$

$ \displaystyle {{\lambda }_{1}}^{2}+{{\lambda }_{2}}^{2}+{{\lambda }_{3}}^{2}+2{{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}}=2({{\lambda }_{1}}{{\lambda }_{2}}+{{\lambda }_{2}}{{\lambda }_{3}}+{{\lambda }_{1}}{{\lambda }_{3}})$

$ \displaystyle \text{Dividing}\ \text{both}\ \text{sides}\ by\ {{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}}\ \text{gives}\ $

$ \displaystyle \frac{{{{\lambda }_{1}}}}{{{{\lambda }_{2}}{{\lambda }_{3}}}}+\frac{{{{\lambda }_{2}}}}{{{{\lambda }_{1}}{{\lambda }_{3}}}}+\frac{{{{\lambda }_{3}}}}{{{{\lambda }_{1}}{{\lambda }_{2}}}}+2=2(\frac{1}{{{{\lambda }_{1}}}}+\frac{1}{{{{\lambda }_{2}}}}+\frac{1}{{{{\lambda }_{3}}}})$

$ \displaystyle \text{Putting}\ \text{the}\ \text{values}\ \text{of}\ {{\lambda }_{1}}\ ,\ {{\lambda }_{2}}\ ,\ {{\lambda }_{3}}\ \ \text{gives}$

$ \displaystyle \frac{{{{{({{k}_{4}}+{{k}_{1}})}}^{2}}}}{{2{{k}_{4}}^{2}}}+\frac{{{{{({{k}_{4}}+{{k}_{2}})}}^{2}}}}{{2{{k}_{4}}^{2}}}+\frac{{{{{({{k}_{4}}+{{k}_{3}})}}^{2}}}}{{2{{k}_{4}}^{2}}}+2$

$ \displaystyle =2\ [\ \frac{{({{k}_{4}}+{{k}_{2}})({{k}_{4}}+{{k}_{3}})}}{{2{{k}_{4}}^{2}}}+\frac{{({{k}_{4}}+{{k}_{1}})({{k}_{4}}+{{k}_{3}})}}{{2{{k}_{4}}^{2}}}+\frac{{({{k}_{4}}+{{k}_{1}})({{k}_{4}}+{{k}_{2}})}}{{2{{k}_{4}}^{2}}}\ ]$

$ \displaystyle {{k}_{1}}^{2}+{{k}_{2}}^{2}+{{k}_{3}}^{2}+2{{k}_{4}}({{k}_{1}}+{{k}_{2}}+{{k}_{3}})+7{{k}_{4}}^{2}=6{{k}_{4}}^{2}+4{{k}_{4}}({{k}_{1}}+{{k}_{2}}+{{k}_{3}})+2({{k}_{1}}{{k}_{2}}+{{k}_{2}}{{k}_{3}}+{{k}_{1}}{{k}_{3}})$

$ \displaystyle {{k}_{1}}^{2}+{{k}_{2}}^{2}+{{k}_{3}}^{2}+{{k}_{4}}^{2}=2{{k}_{4}}({{k}_{1}}+{{k}_{2}}+{{k}_{3}})+2({{k}_{1}}{{k}_{2}}+{{k}_{2}}{{k}_{3}}+{{k}_{1}}{{k}_{3}})$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ={{({{k}_{1}}+{{k}_{2}}+{{k}_{3}}+{{k}_{4}})}^{2}}-({{k}_{1}}^{2}+{{k}_{2}}^{2}+{{k}_{3}}^{2}+{{k}_{4}}^{2})$

$ \displaystyle \therefore \ {{({{k}_{1}}+{{k}_{2}}+{{k}_{3}}+{{k}_{4}})}^{2}}=2({{k}_{1}}^{2}+{{k}_{2}}^{2}+{{k}_{3}}^{2}+{{k}_{4}}^{2})$

In the figure below , semicircles with centres at A and B and with radii 2 and 1 respectively,are drawn in the interior of , and sharing bases with , a semicircle with diameter JK . The two smaller semicircles are externally tangent to each other and internally tangent to each other and internally tangent to the largest semicircle . A circle centred at P is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle . What is the radius of the circle centred at P .
 

Solution
$ \displaystyle {{r}_{1}}=1\ ,\ {{r}_{2}}\ =2\ ,\ {{r}_{3}}=3$

$ \displaystyle {{k}_{1}}=\frac{1}{{{{r}_{1}}}}=1\ ,\ {{k}_{2}}=\frac{1}{{{{r}_{2}}}}=\frac{1}{2}\ \ ,\ {{k}_{3}}=-\frac{1}{{{{r}_{3}}}}=-\frac{1}{3}$

By Descartes' Circle Theorem ,

$ \displaystyle {{({{k}_{1}}+{{k}_{2}}+{{k}_{3}}+{{k}_{4}})}^{2}}=2({{k}_{1}}^{2}+{{k}_{2}}^{2}+{{k}_{3}}^{2}+{{k}_{4}}^{2})$

$ \displaystyle {{(1+\frac{1}{2}-\frac{1}{3}+\frac{1}{{{{r}_{4}}}})}^{2}}=2(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{{{{r}_{4}}^{2}}})$

$ \displaystyle {{(\frac{{7{{r}_{4}}+6}}{{6{{r}_{4}}}})}^{2}}=2(\frac{{49{{r}_{4}}^{2}+36}}{{36{{r}_{4}}^{2}}})$

$ \displaystyle 49{{r}_{4}}^{2}+84{{r}_{4}}+36=98{{r}_{4}}^{2}+72$

$ \displaystyle 49{{r}_{4}}^{2}-84{{r}_{4}}+36=0$

$ \displaystyle {{(7{{r}_{4}}-6)}^{2}}=0$

$ \displaystyle \ \ \ \ 7{{r}_{4}}-6=0$

$ \displaystyle \ \ \ \ \therefore \ \ \ {{r}_{4}}=\frac{6}{7}$

Circle: Semicircle circles and Cosines law

In the figure below , semicircles with centres at A and B and with radii 2 and 1 respectively,are drawn in the interior of , and sharing bases with , a semicircle with diameter JK . The two smaller semicircles are externally tangent to each other and internally tangent to each other and internally tangent to the largest semicircle . A circle centred at P is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle . What is the radius of the circle centred at P .

Solution

Let C be centre of largest semicircle .

By the law of cosines ,

$ \displaystyle \cos \theta =\frac{{A{{P}^{2}}+A{{C}^{2}}-P{{C}^{2}}}}{{2\ AP.AC}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{{{{(2+r)}}^{2}}+1-{{{(3-r)}}^{2}}}}{{2(2+r)}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{10r-4}}{{2(2+r)}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{5r-2}}{{2+r}}\ \ \ \ \ \ \ ...........(1)$

$ \displaystyle \cos \theta =\frac{{A{{P}^{2}}+A{{B}^{2}}-P{{B}^{2}}}}{{2\ AP.AB}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{{{{(2+r)}}^{2}}+{{3}^{2}}-{{{(1+r)}}^{2}}}}{{6(2+r)}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{2r+12}}{{6(2+r)}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{r+6}}{{3(2+r)}}\ \ \ \ \ \ \ ...........(2)$

$ \displaystyle \text{From}\ (1)\ \text{and}\ (2)\ ,\ \ \ \ \frac{{5r-2}}{{2+r}}=\frac{{r+6}}{{3(2+r)}}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 15r-6=r+6$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 14r=12$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore \ \ r=\frac{6}{7}$

Circle: Common tangents of circles

Given : AB and MN are common tangents of circles O and P . AB = 15 and MN = 5 .
Find : the product of $ \displaystyle {{r}_{1}}\ and\ {{r}_{2}}$ .

Solution

NM produced meet AB at C .

Join OA , OC , OP , PC , PB and draw $ \displaystyle OD\bot PB$ .

$ \displaystyle \text{Let}\ AC=CM=x$

$ \displaystyle \ \ \ \ \ \ CN=CB\ \ (\ \because \ \text{tangents}\ )$

$ \displaystyle \ \ \ \ \ \ x+5=15-x$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ x=5$

$ \displaystyle \ \ \ 2\theta +2\beta ={{180}^{\circ }}$

$ \displaystyle \ \ \ \ \ \ \theta +\beta ={{90}^{\circ }}$

$ \displaystyle \text{In}\ \text{rt}\ \Delta OCP\ ,\ O{{P}^{2}}=O{{C}^{2}}+C{{P}^{2}}$

$ \displaystyle \text{In}\ \text{rt}\ \Delta ODP\ ,\ O{{P}^{2}}=O{{D}^{2}}+D{{P}^{2}}$

$ \displaystyle \ \ \ \ \ O{{C}^{2}}+C{{P}^{2}}=O{{D}^{2}}+D{{P}^{2}}$

$ \displaystyle \ ({{r}_{1}}^{2}+{{5}^{2}})+({{r}_{2}}^{2}+{{10}^{2}})={{15}^{2}}+{{({{r}_{2}}-{{r}_{1}})}^{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 125=225-2{{r}_{1}}{{r}_{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 2{{r}_{1}}{{r}_{2}}=100$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore \ {{r}_{1}}{{r}_{2}}=50$


 
 

Circle: Area of triangle and cosines law

Given : In circle O , $ \displaystyle AB=\sqrt{{41}}\ ,\ AC=5\ ,\ BC=8$ and $ \displaystyle A{{A}^{'}}$ is a diameter and as shown in figure .
Find : area of triangle $ \displaystyle {{A}^{'}}BC$ .

Solution

$ \displaystyle AB=\sqrt{{41}}\ ,\ AC=5\ ,\ BC=8$

$ \displaystyle \text{Draw}\ {{A}^{'}}D\bot BC.$ 

$ \displaystyle A{{B}^{2}}+{{A}^{'}}{{B}^{2}}=A{{C}^{2}}+{{A}^{'}}{{C}^{2}}$

$ \displaystyle 41+{{A}^{'}}{{D}^{2}}+B{{D}^{2}}=25+{{A}^{'}}{{D}^{2}}+D{{C}^{2}}$

$ \displaystyle D{{C}^{2}}-B{{D}^{2}}=16$ 

$ \displaystyle 8\ (DC-BD)=16$ 

$ \displaystyle \ \ \ \ \ DC-BD=2$

$ \displaystyle \therefore \ BD=3\ \ ,\ \ DC=5$ 

$ \displaystyle \text{By}\ \text{the}\ \text{law}\ \text{of}\ \text{cosines}\ ,$ 

$ \displaystyle \cos \theta =\frac{{A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}}}{{2AB.BC}}$

$ \displaystyle \ \ \ \ \ \ \ =\frac{{41+64-25}}{{16\sqrt{{41}}}}$ 

$ \displaystyle \ \ \ \ \ \ \ =\frac{5}{{\sqrt{{41}}}}$ 

$ \displaystyle \sin ({{90}^{\circ }}-\theta )=\frac{5}{{\sqrt{{41}}}}\ \ \ \ \ \left[ {\because \sin ({{{90}}^{\circ }}-\theta )=\cos \theta } \right]$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \frac{{{{A}^{'}}D}}{{{{A}^{'}}B}}=\frac{5}{{\sqrt{{41}}}}\ $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \frac{{{{A}^{'}}{{D}^{2}}}}{{{{A}^{'}}{{B}^{2}}}}=\frac{{25}}{{41}}$

$ \displaystyle \ \ \ \ \ \frac{{{{A}^{'}}{{D}^{2}}}}{{{{A}^{'}}{{D}^{2}}+9}}=\frac{{25}}{{41}}$ 

$ \displaystyle 41\ {{A}^{'}}{{D}^{2}}=25\ {{A}^{'}}{{D}^{2}}+\ 225$ 

$ \displaystyle \ \ \ {{A}^{'}}{{D}^{2}}=\frac{{225}}{{16}}$

$ \displaystyle \ \ \ \ {{A}^{'}}D=\frac{{15}}{4}$ 

$ \displaystyle \therefore \ \alpha \ (\ \Delta \ {{A}^{'}}BC\ )=\frac{1}{2}\ \times \ BC\ \times \ {{A}^{'}}D$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{1}{2}\ \times \ 8\ \times \ \frac{{15}}{4}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =15\ \ \text{sq}\ \text{units}$

Circle: Beautiful problem

Three circles touch the same straight line and touch each other, as shown . Prove that the radii  a , b and c , where c is smallest , satisfy the equation $ \displaystyle \frac{1}{{\sqrt{a}}}+\frac{1}{{\sqrt{b}}}=\frac{1}{{\sqrt{c}}}$ .

Solution

$ \displaystyle \text{Let}\ PC=x\ \ ,\ DQ=y\ \ \ ,\ \ QE=z$ 

$ \displaystyle \text{In}\ \text{rt}\ \Delta OCP\ ,\ \ O{{P}^{2}}=O{{C}^{2}}+P{{C}^{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{(a+b)}^{2}}={{(a-b)}^{2}}+{{x}^{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{x}^{2}}=4ab$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x=2\sqrt{{ab}}$

$ \displaystyle \text{In}\ \text{rt}\ \Delta ODQ\ ,\ \ {{y}^{2}}=O{{Q}^{2}}-O{{D}^{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{y}^{2}}={{(a+c)}^{2}}-{{(a-c)}^{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{y}^{2}}=4ac$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ y=2\sqrt{{ac}}$

$ \displaystyle \text{In}\ \text{rt}\ \Delta QEP\ ,\ \ \ {{z}^{2}}=Q{{P}^{2}}-P{{E}^{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{z}^{2}}={{(b+c)}^{2}}-{{(b-c)}^{2}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{z}^{2}}=4bc$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ z=2\sqrt{{bc}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ x=y+z$

$ \displaystyle \ \ \ \ 2\sqrt{{ab}}=2\sqrt{{ac}}+2\sqrt{{bc}}$

$ \displaystyle \ \ \ \ \ \sqrt{{ab}}=\sqrt{{ac}}+\sqrt{{bc}}$

$ \displaystyle \ \ \ \ \ \frac{{\sqrt{{ab}}}}{{\sqrt{{abc}}}}=\frac{{\sqrt{{ac}}}}{{\sqrt{{abc}}}}+\frac{{\sqrt{{bc}}}}{{\sqrt{{abc}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ \frac{1}{{\sqrt{c}}}=\frac{1}{{\sqrt{b}}}+\frac{1}{{\sqrt{a}}}$

$ \displaystyle \ \therefore \ \ \ \frac{1}{{\sqrt{a}}}+\frac{1}{{\sqrt{b}}}=\frac{1}{{\sqrt{c}}}$

*Note
      If two circles are tangent internally or externally , the line containing their centres also   contains the point of tangency . 

Area of the region: Area of equilateral triangle and area of a sector

In the figure shown , US and UT are line segments each of length  2 , and $\displaystyle \angle TUS={{60}^{\circ }}$ . Arcs TR and SR are each one - sixth of a circle with radius 2 . What is the area of the region shown ?

Solution

 $ \displaystyle \alpha (\Delta UVW)=\frac{{\sqrt{3}}}{4}\times {{4}^{2}}$

$ \displaystyle \text{Area}\ \text{of}\ \text{sector}\ VSR\ =\ \text{Area}\ \text{of}\ \text{sector}\ WRT\ =\ \frac{1}{2}\times {{2}^{2}}\times \frac{\pi }{3}$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{2\pi }}{3}$

$ \displaystyle \therefore \ The\ area\ of\ the\ region\ =\ \alpha (\Delta UVW)\ -\ [\text{Area}\ \text{of}\ \text{sector}\ VSR\ +\ \text{Area}\ \text{of}\ \text{sector}\ WRT\ ]$ 

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ (4\sqrt{3}-\frac{{4\pi }}{3})\ \ \text{sq}\ \ \text{units}$ 

*Note

 

 

Calculus: Maximum and minimum

The diagram below show three right-angle triangles, where $ \displaystyle BC=14,GF=10,DE=7$ and $ \displaystyle \angle BCA=\angle BDE=\angle FGD=\theta $ . Find the maximum possible value of $ \displaystyle AB+BD+DF$.

Solution

$ \displaystyle BC=14,GF=10,DE=7$

$ \displaystyle \angle BCA=\angle BDE=\angle FGD=\theta $

$ \displaystyle \text{Let}\ \ \ y=AB+BD+DF$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ =14\sin \theta +7\cos \theta +10\sin \theta $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ =24\sin \theta +7\cos \theta $

$ \displaystyle \ \ \ \ \ \frac{{dy}}{{d\theta }}=24\cos \theta -7\sin \theta $

$ \displaystyle \text{For}\ \text{stationary}\ \text{value}\ ,\ \frac{{dy}}{{d\theta }}=0$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ 24\cos \theta -7\sin \theta =0$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 24\cos \theta =7\sin \theta $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \tan \theta =\frac{{24}}{7}$

$ \displaystyle \ \ \ \ \ \frac{{{{d}^{2}}y}}{{d{{\theta }^{2}}}}=-24\sin \theta -7\cos \theta $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ =-\cos \theta \ (24\tan \theta -7)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ =-\cos \theta \ (\frac{{576}}{7}-7)$

$ \displaystyle \text{Since }\ \theta \ \ \text{is}\ \text{acute}\ ,\ \frac{{{{d}^{2}}y}}{{d{{\theta }^{2}}}}<0\ (\text{maximum})$

$ \displaystyle \text{The}\ \text{maximum}\ \text{possible}\ \text{value}\ \text{of}\ AB+BD+DF$

$ \displaystyle =24\sin \theta +7\cos \theta $

$ \displaystyle =24(\frac{{24}}{{25}})+7(\frac{7}{{25}})$

$ \displaystyle =\frac{{576}}{{25}}+\frac{{49}}{{25}}$

$\displaystyle =\frac{{625}}{{25}}=25$

Pythagoras Theorem and Cosines Law

ABCD is a square . If $ \displaystyle BC=1\ \ \text{and  }a+b+c=2$ , find x .

Solution

By the Pythagoras theorem ,

$ \displaystyle {{a}^{2}}+{{b}^{2}}={{c}^{2}}$

$ \displaystyle a+b+c=2$

$ \displaystyle {{(a+b)}^{2}}={{(2-c)}^{2}}$

$ \displaystyle {{a}^{2}}+2ab+{{b}^{2}}=4-4c+{{c}^{2}}$

$ \displaystyle ab=2-2c\ \ \ (\because {{a}^{2}}+{{b}^{2}}={{c}^{2}})$

By the law of cosines ,

$ \displaystyle \cos x=\frac{{2-2a+{{a}^{2}}+2-2b+{{b}^{2}}-{{c}^{2}}}}{{2\sqrt{{(2-2a+{{a}^{2}})(2-2b+{{b}^{2}})}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{{2-a-b}}{{\sqrt{{4-4b+2{{b}^{2}}-4a+4ab-2a{{b}^{2}}+2{{a}^{2}}-2{{a}^{2}}b+{{a}^{2}}{{b}^{2}}}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{c}{{\sqrt{{4(1-b-a+ab)+2({{a}^{2}}+{{b}^{2}})-2ab(a+b)+{{{(2-2c)}}^{2}}}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{c}{{\sqrt{{4(1-c)+2{{c}^{2}}-2(4-6c+2{{c}^{2}})+4-8c+4{{c}^{2}}}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{c}{{\sqrt{{8-12c+6{{c}^{2}}-8+12c-4{{c}^{2}}}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{c}{{\sqrt{{2{{c}^{2}}}}}}$

$ \displaystyle \ \ \ \ \ \ \ \ =\frac{1}{{\sqrt{2}}}=\cos {{45}^{\circ }}\ $

$ \displaystyle \therefore \ \ x={{45}^{\circ }}$

Vector: Regular octagon

Solution

$ \displaystyle \overrightarrow{{AB}}=\overrightarrow{p}\ \ \ ,\ \ \overrightarrow{{BC}}=\overrightarrow{q}$

$ \displaystyle \overrightarrow{{AH}}=\overrightarrow{{AP}}+\overrightarrow{{PH}}$

$ \displaystyle \ \ \ \ \ \ =-\frac{1}{{\sqrt{2}}}\overrightarrow{p}+\overrightarrow{{QC}}$

$ \displaystyle \ \ \ \ \ \ =-\frac{1}{{\sqrt{2}}}\overrightarrow{p}+\overrightarrow{{QB}}+\overrightarrow{{BC}}$

$ \displaystyle \ \ \ \ \ \ =-\frac{1}{{\sqrt{2}}}\overrightarrow{p}-\frac{1}{{\sqrt{2}}}\overrightarrow{p}+\overrightarrow{q}$

$ \displaystyle \ \ \ \ \ \ =\overrightarrow{q}-\sqrt{2}\ \overrightarrow{p}$

$ \displaystyle \overrightarrow{{AE}}+\overrightarrow{{BH}}+\overrightarrow{{CG}}+\overrightarrow{{DF}}$

$ \displaystyle =(\overrightarrow{{AH}}+\overrightarrow{{HE}})+\overrightarrow{{BH}}+(\overrightarrow{{CF}}+\overrightarrow{{FG}})+\overrightarrow{{BH}}$

$ \displaystyle =\overrightarrow{{AH}}+\overrightarrow{{HE}}+2\overrightarrow{{BH}}+\overrightarrow{{CF}}+\overrightarrow{{FG}}$

$ \displaystyle =\overrightarrow{{AH}}+(1+\sqrt{2})\overrightarrow{q}+2(\overrightarrow{{BA}}+\overrightarrow{{AH}})+(1+\sqrt{2})\overrightarrow{{DE}}-\overrightarrow{q}$

$ \displaystyle =\overrightarrow{{AH}}+\sqrt{2}\ \overrightarrow{q}-2\overrightarrow{p}+2\overrightarrow{{AH}}+(1+\sqrt{2})\overrightarrow{{AH}}$

$ \displaystyle =(4+\sqrt{2})\overrightarrow{{AH}}+\sqrt{2}\ \overrightarrow{q}-2\overrightarrow{p}$

$ \displaystyle =(4+\sqrt{2})(\overrightarrow{q}-\sqrt{2}\ \overrightarrow{p})+\sqrt{2}(\overrightarrow{q}-\sqrt{2}\ \overrightarrow{p})$

$ \displaystyle =(4+2\sqrt{2})(\overrightarrow{q}-\sqrt{2}\ \overrightarrow{p})$

$ \displaystyle =2(2+\sqrt{2})(\overrightarrow{q}-\sqrt{2}\ \overrightarrow{p})$

Vector

ABCDE is a regular pentagon . If $ \displaystyle \overrightarrow{{AB}}\ =\overrightarrow{a}$ and $ \displaystyle \overrightarrow{{BC}}\ =\overrightarrow{b}$, find $ \displaystyle \overrightarrow{{CD}}\ ,\overrightarrow{{DE}}\ \text{and }\overrightarrow{{EA}}$ in terms of $ \displaystyle \overrightarrow{a}\ \ \text{and }\overrightarrow{b}$.

Solution

$ \displaystyle \overrightarrow{{AB}}=\overrightarrow{a}\ \ ,\ \ \overrightarrow{{BC}}=\overrightarrow{b}$

$ \displaystyle \overrightarrow{{FC}}=-\frac{{1+\sqrt{5}}}{2}\overrightarrow{a}+\overrightarrow{b}$

$ \displaystyle \overrightarrow{{CD}}=\frac{2}{{1+\sqrt{5}}}\overrightarrow{{FC}}$

$ \displaystyle \ \ \ \ \ =-\overrightarrow{a}+\frac{2}{{1+\sqrt{5}}}\overrightarrow{b}$

$ \displaystyle \overrightarrow{{GD}}=-\frac{{1+\sqrt{5}}}{2}\overrightarrow{b}+\frac{2}{{1+\sqrt{5}}}\overrightarrow{b}-\overrightarrow{a}$

$ \displaystyle \ \ \ \ \ =-\overrightarrow{b}-\overrightarrow{a}$

$ \displaystyle \overrightarrow{{DE}}=\frac{2}{{1+\sqrt{5}}}\overrightarrow{{GD}}$

$ \displaystyle \ \ \ \ \ =-\frac{2}{{1+\sqrt{5}}}(\overrightarrow{a}+\overrightarrow{b})$

$ \displaystyle \overrightarrow{{HE}}=\overrightarrow{{HD}}+\overrightarrow{{DE}}$

$ \displaystyle \ \ \ \ \ \ =-\frac{{1+\sqrt{5}}}{2}\overrightarrow{{CD}}-\frac{2}{{1+\sqrt{5}}}(\overrightarrow{a}+\overrightarrow{b})$

$ \displaystyle \ \ \ \ \ =\frac{{1+\sqrt{5}}}{2}\overrightarrow{a}-\overrightarrow{b}-\frac{2}{{1+\sqrt{5}}}\overrightarrow{a}-\frac{2}{{1+\sqrt{5}}}\overrightarrow{b}$

$ \displaystyle \ \ \ \ \ =\overrightarrow{a}-\frac{{3+\sqrt{5}}}{{1+\sqrt{5}}}\overrightarrow{b}$

$\displaystyle \overrightarrow{{EA}}=\frac{2}{{1+\sqrt{5}}}\overrightarrow{{HE}}$

$ \displaystyle \ \ \ \ \ =\frac{2}{{1+\sqrt{5}}}\overrightarrow{a}-\overrightarrow{b}$

Geometry

Two intersecting circles $ \displaystyle {{C}_{1}}\ \text{and  }{{C}_{2}}$ have a common tangent which touches $ \displaystyle {{C}_{1}}\ \text{at  }P\ \ \text{and  }{{C}_{2}}\ \ \text{at  }Q$. The two circles intersect at M and N , where N is nearer to PQ then M . The line PN meets the circle $ \displaystyle \text{ }{{C}_{2}}$ again at R . Prove that MQ bisects $ \displaystyle \angle PMR$ .

$ \displaystyle \text{Proof : Join  }MN\text{  and   }QR.$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \theta =\beta \ \ (\text{angle between tangent and chord = }$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{angle in the alternate segment )}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \phi =\gamma \ \ \ \ \text{( same arc }QN\ )$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \text{In }\Delta \ PQR,\ \ \ \theta +\phi =\Omega $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \beta +\gamma =\Omega $

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \Omega =\alpha \text{ }\ (\text{angle between tangent and chord = }$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{angle in the alternate segment )}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \beta +\gamma =\alpha $

$ \displaystyle \ \ \ \ \ \ \ \ \ \therefore \ MQ\ \ \text{bisects   }\angle PMR.$

A.P and G.P

Adding the corresponding terms of an A.P and G.P makes the new sequence 1,7,6,9,... .
Find the $ \displaystyle {{n}^{{th}}}$ term of this sequence .

Solution

Let $ \displaystyle a,a+d,a+2d,a+3d,...\ \text{is an }A.P\text{  and}$

$ \displaystyle A,Ar,A{{r}^{2}},A{{r}^{3}},...\ \text{is a }G.P\ .$

$ \displaystyle a+A,a+d+Ar,a+2d+A{{r}^{2}},a+3d+A{{r}^{3}},...=1,7,6,9,...$

$ \displaystyle a+A=1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ......(1)$

$\displaystyle a+d+Ar=7\ \ \ \ \ \ \ ......(2)$

$ \displaystyle a+2d+A{{r}^{2}}=6\ \ \ \ \ .....(3)$

$ \displaystyle a+3d+A{{r}^{3}}=9\ \ \ \ \ .....(4)$

$ \displaystyle (2)-(1)\Rightarrow \ \ \ d+Ar-A=6\ \ \ \ \ \ \ .......(5)$

$ \displaystyle (3)-(2)\Rightarrow \ \ \ d+A{{r}^{2}}-Ar=-1\ ........(6)$

$ \displaystyle (4)-(3)\Rightarrow \ \ \ d+A{{r}^{3}}-A{{r}^{2}}=3\ \ ........(7)$

$ \displaystyle (6)-(5)\Rightarrow \ \ \ A{{r}^{2}}-2Ar+A=-7$

$ \displaystyle (7)-(6)\Rightarrow \ \ \ A{{r}^{3}}-2A{{r}^{2}}+Ar=4$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ r(A{{r}^{2}}-2Ar+A)=4$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -7r=4$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ r=-\frac{4}{7}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{16}}{{49}}A+\frac{8}{7}A+A=-7$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 16A+56A+49A=-343$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ A=-\frac{{343}}{{121}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ a=1+\frac{{343}}{{121}}=\frac{{464}}{{121}}\ \ \ \ \ \left[ {By(1)} \right]$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ d+\frac{{196}}{{121}}+\frac{{343}}{{121}}=6\ \ \ \ \ \ \ \left[ {By(5)} \right]$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ d=\frac{{187}}{{121}}$

$ \displaystyle \text{The }{{\text{n}}^{{th}}}\text{ term of given sequence = }{{u}_{n}}$

$ \displaystyle \ \ \ {{u}_{n}}=a+(n-1)d+A{{r}^{{n-1}}}$

$ \displaystyle \ \ \ \ \ \ =\frac{{464}}{{121}}+(n-1)\frac{{187}}{{121}}+(-\frac{{343}}{{121}}){{(-\frac{4}{7})}^{{n-1}}}$

$ \displaystyle \ \ \ \ \ \ =\frac{1}{{121}}\left[ {277+187n-343{{{(-\frac{4}{7})}}^{{n-1}}}} \right]$

R(1)

If $ \displaystyle \alpha $ and $ \displaystyle \beta $ are the roots of the equations $ \displaystyle {{x}^{2}}+px+q=0$ and $\displaystyle {{x}^{{2n}}}+{{p}^{n}}{{x}^{n}}+{{q}^{n}}=0$ , where $ \displaystyle n$ is an even integer . Prove that $ \displaystyle \frac{\alpha }{\beta }$ and $ \displaystyle \frac{\beta }{\alpha }$ are the roots of the equation $ \displaystyle {{x}^{n}}+1+{{(x+1)}^{n}}=0$ .

Solution

$ \displaystyle {{x}^{2}}+px+q=0$

$ \displaystyle \alpha \ \ \text{and  }\beta \ \ \ \text{are the roots of the equation }\text{.}$

$ \displaystyle p=-(\alpha +\beta )\ \ \text{and   }q=\alpha \beta $

$ \displaystyle {{x}^{{2n}}}+{{p}^{n}}{{x}^{n}}+{{q}^{n}}=0$

$ \displaystyle \alpha \ \ \text{and  }\beta \ \ \ \text{are the roots of the equation }\text{.}$

$ \displaystyle {{\alpha }^{{2n}}}+{{p}^{n}}{{\alpha }^{n}}+{{q}^{n}}=0\ \ \ \text{and   }{{\beta }^{{2n}}}+{{p}^{n}}{{\beta }^{n}}+{{q}^{n}}=0\text{ }$

$ \displaystyle {{\alpha }^{{2n}}}+{{p}^{n}}{{\alpha }^{n}}={{\beta }^{{2n}}}+{{p}^{n}}{{\beta }^{n}}$

$ \displaystyle {{\alpha }^{{2n}}}-{{\beta }^{{2n}}}={{p}^{n}}({{\beta }^{n}}-{{\alpha }^{n}})$

$ \displaystyle ({{\alpha }^{n}}-{{\beta }^{n}})({{\alpha }^{n}}+{{\beta }^{n}})={{(\alpha +\beta )}^{n}}({{\beta }^{n}}-{{\alpha }^{n}})\ \left[ {\because n\ \text{is even integer}} \right]$

$ \displaystyle {{\alpha }^{n}}+{{\beta }^{n}}=-{{(\alpha +\beta )}^{n}}$

$ \displaystyle \text{Let  }f(x)={{x}^{n}}+1+{{(x+1)}^{n}}$

$ \displaystyle \ \ \ \ \ f(\frac{\alpha }{\beta })={{(\frac{\alpha }{\beta })}^{n}}+1+{{(\frac{\alpha }{\beta }+1)}^{n}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{{{\alpha }^{n}}+{{\beta }^{n}}+{{{(\alpha +\beta )}}^{n}}}}{{{{\beta }^{n}}}}=0$

$ \displaystyle \ \ \ \ \ f(\frac{\beta }{\alpha })={{(\frac{\beta }{\alpha })}^{n}}+1+{{(\frac{\beta }{\alpha }+1)}^{n}}$

$\displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{{{\beta }^{n}}+{{\alpha }^{n}}+{{{(\alpha +\beta )}}^{n}}}}{{{{\alpha }^{n}}}}=0$

$ \displaystyle \therefore \frac{\alpha }{\beta }\ \ \text{and  }\frac{\beta }{\alpha }\ \ \text{are the roots of the equation }{{x}^{n}}+1+{{(x+1)}^{n}}=0.$

P(1)

A spinner has four sectors whose angles form a G.P . The smallest angle is $\displaystyle {{24}^{\circ }}$ and the sector are numbered as 1,2,3,4 in ascending order of their degree measures . If the arrow is spun 720 times what final score would you expect when all the individual scores are added together ?

Solution

Let the four angles be $ \displaystyle {{24}^{\circ }},{{24}^{\circ }}r,{{24}^{\circ }}{{r}^{2}},{{24}^{\circ }}{{r}^{3}}$ .

$ \displaystyle {{24}^{\circ }}+{{24}^{\circ }}r+{{24}^{\circ }}{{r}^{2}}+{{24}^{\circ }}{{r}^{3}}={{360}^{\circ }}$

$ \displaystyle {{1}^{\circ }}+r+{{r}^{2}}+{{r}^{3}}={{15}^{\circ }}$

$ \displaystyle {{r}^{3}}+{{r}^{2}}+r-{{14}^{\circ }}=0$

$ \displaystyle (r-{{2}^{\circ }})({{r}^{2}}+3r+{{7}^{\circ }})=0$

$ \displaystyle r-{{2}^{\circ }}=0\ \ \ \ (or)\ \ \ \ {{r}^{2}}+3r+{{7}^{\circ }}=0$

$ \displaystyle \ \ \ \ \ \ r={{2}^{\circ }}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (reject)\ (\because {{b}^{2}}-4ac<0)$

$ \displaystyle \text{The four angles are 2}{{\text{4}}^{\circ }},{{48}^{\circ }},{{96}^{\circ }}\text{  and  }{{192}^{\circ }}.$

$ \displaystyle \text{Final score = }(1\times \frac{1}{{15}}\times 720)+(2\times \frac{2}{{15}}\times 720)+$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3\times \frac{4}{{15}}\times 720)+(4\times \frac{8}{{15}}\times 720)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =720(\frac{1}{{15}}+\frac{4}{{15}}+\frac{{12}}{{15}}+\frac{{32}}{{15}})$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =720\times \frac{{49}}{{15}}=2352$

M (1)

Given that $ \displaystyle A=\left( {\begin{array}{*{20}{c}} {\frac{1}{2}} & 1 \\ 0 & {\frac{1}{3}} \end{array}} \right)\ \ $ , find $ \displaystyle {{A}^{n}}$ , where $ \displaystyle n$ is a natural number. If $ \displaystyle \ \ B=A+{{A}^{2}}+{{A}^{3}}+{{A}^{4}}+...\ \ $ , then find $ \displaystyle \ {{B}^{{-1}}}$ .

Solution

$ \displaystyle {{A}^{n}}=\left( {\begin{array}{*{20}{c}} {\frac{1}{2}} & 1 \\ 0 & {\frac{1}{3}} \end{array}} \right)\ =\left( {\begin{array}{*{20}{c}} {\frac{1}{2}} & {6(\frac{1}{2}-\frac{1}{3})} \\ 0 & {\frac{1}{3}} \end{array}} \right)\ $

$ \displaystyle {{A}^{2}}=\ \left( {\begin{array}{*{20}{c}} {\frac{1}{2}} & 1 \\ 0 & {\frac{1}{3}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\frac{1}{2}} & 1 \\ 0 & {\frac{1}{3}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {\frac{1}{4}} & {\frac{5}{6}} \\ 0 & {\frac{1}{9}} \end{array}} \right)\ =\left( {\begin{array}{*{20}{c}} {\frac{1}{{{{2}^{2}}}}} & {6(\frac{1}{{{{2}^{2}}}}-\frac{1}{{{{3}^{2}}}})} \\ 0 & {\frac{1}{{{{3}^{2}}}}} \end{array}} \right)\ $

$ \displaystyle {{A}^{3}}=\left( {\begin{array}{*{20}{c}} {\frac{1}{4}} & {\frac{5}{6}} \\ 0 & {\frac{1}{9}} \end{array}} \right)\ \left( {\begin{array}{*{20}{c}} {\frac{1}{2}} & 1 \\ 0 & {\frac{1}{3}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {\frac{1}{8}} & {\frac{{19}}{{36}}} \\ 0 & {\frac{1}{{27}}} \end{array}} \right)\ =\left( {\begin{array}{*{20}{c}} {\frac{1}{{{{2}^{3}}}}} & {6(\frac{1}{{{{2}^{3}}}}-\frac{1}{{{{3}^{3}}}})} \\ 0 & {\frac{1}{{{{3}^{3}}}}} \end{array}} \right)\ $

$ \displaystyle {{A}^{4}}=\ \left( {\begin{array}{*{20}{c}} {\frac{1}{8}} & {\frac{{19}}{{36}}} \\ 0 & {\frac{1}{{27}}} \end{array}} \right)\ \left( {\begin{array}{*{20}{c}} {\frac{1}{2}} & 1 \\ 0 & {\frac{1}{3}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {\frac{1}{{16}}} & {\frac{{65}}{{216}}} \\ 0 & {\frac{1}{{81}}} \end{array}} \right)=\left( {\begin{array}{*{20}{c}} {\frac{1}{{{{2}^{4}}}}} & {6(\frac{1}{{{{2}^{4}}}}-\frac{1}{{{{3}^{4}}}})} \\ 0 & {\frac{1}{{{{3}^{4}}}}} \end{array}} \right)$
.
.
.
$ \displaystyle {{A}^{n}}=\left( {\begin{array}{*{20}{c}} {\frac{1}{{{{2}^{n}}}}} & {6(\frac{1}{{{{2}^{n}}}}-\frac{1}{{{{3}^{n}}}})} \\ 0 & {\frac{1}{{{{3}^{n}}}}} \end{array}} \right)\ $

$ \displaystyle B=A+{{A}^{2}}+{{A}^{3}}+{{A}^{4}}+...\ $

$ \displaystyle B=\left( {\begin{array}{*{20}{c}} {\frac{1}{2}+\frac{1}{{{{2}^{2}}}}+\frac{1}{{{{2}^{3}}}}+\frac{1}{{{{2}^{4}}}}+...} & {6((\frac{1}{2}+\frac{1}{{{{2}^{2}}}}+\frac{1}{{{{2}^{3}}}}+\frac{1}{{{{2}^{4}}}}+...)-(\frac{1}{3}+\frac{1}{{{{3}^{2}}}}+\frac{1}{{{{3}^{3}}}}+\frac{1}{{{{3}^{4}}}}+...))} \\ 0 & {\frac{1}{3}+\frac{1}{{{{3}^{2}}}}+\frac{1}{{{{3}^{3}}}}+\frac{1}{{{{3}^{4}}}}+...} \end{array}} \right)\ $

$ \displaystyle B=\left( {\begin{array}{*{20}{c}} 1 & {6(1-\frac{1}{2})} \\ 0 & {\frac{1}{2}} \end{array}} \right)\ $

$ \displaystyle \therefore B=\ \left( {\begin{array}{*{20}{c}} 1 & 3 \\ 0 & {\frac{1}{2}} \end{array}} \right)\ $

$ \displaystyle \det B=\frac{1}{2}\ -0=\frac{1}{2}\ne 0,\ {{B}^{{-1}}}\ \text{exists }\text{.}$

$ \displaystyle \therefore \ {{B}^{{-1}}}=2\left( {\begin{array}{*{20}{c}} {\frac{1}{2}} & {-3} \\ 0 & 1 \end{array}} \right)\ =\left( {\begin{array}{*{20}{c}} 1 & {-6} \\ 0 & 2 \end{array}} \right)$

Note
$ \displaystyle *\ \ \ \ S=\frac{a}{{1-r}}$

Inverse Function

The function $ \displaystyle f:R\to R$ is defined by $ \displaystyle f(x)={{4}^{x}}-2$ .

$ \displaystyle (a)$ Find the value of $ \displaystyle x$ for which $ \displaystyle f(x)=0$ .

$ \displaystyle (b)\ $ Find the inverse function $ \displaystyle {{f}^{{-1}}}$ , and state the domain of $ \displaystyle {{f}^{{-1}}}$ .


Solution

$ \displaystyle \ \ \ \ \ \ \ \ \ \ f(x)={{4}^{x}}-2$

$ \displaystyle (a)\ \ \ \ \ f(x)=\ 0$

$ \displaystyle \ \ \ \ \ \ \ \ {{4}^{x}}-2=0$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ {{4}^{x}}=2$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ {{2}^{{2x}}}=2$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ 2x=1$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x=\frac{1}{2}$

$ \displaystyle (b)\ \ \ \ Let\ \ {{f}^{{-1}}}(x)=y$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x=f(y)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x={{4}^{y}}-2$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{4}^{y}}=x+2$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ y={{\log }_{4}}(x+2)$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{f}^{{-1}}}(x)={{\log }_{4}}(x+2)\ ,\ x>-2$

$ \displaystyle \text{The domain of  }{{f}^{{-1}}}=\{x/x\in R,x>-2\}$

G.P

A G.P has first term and common ratio both equal to $ \displaystyle \alpha ,\alpha >1$.Given that the sum of the first 12 terms is 28 times the sum of the first 6 terms , find the exact value of  $ \displaystyle \alpha $.
Hence evaluate $ \displaystyle {{\log }_{3}}(\frac{3}{2}{{\alpha }^{2}}+{{\alpha }^{4}}+{{\alpha }^{6}}+...+{{\alpha }^{{58}}})$ giving your answer in the form of $ \displaystyle A-{{\log }_{3}}B$ , where A and B are positive integers to be determined.

Solution

$ \displaystyle a=r=\alpha \ \ \ ,\ \ \ \alpha >1$

$ \displaystyle {{S}_{{12}}}=28\ {{S}_{6}}$

$ \displaystyle \frac{{a({{r}^{{12}}}-1)}}{{r-1}}=28\times \frac{{a({{r}^{6}}-1)}}{{r-1}}$

$ \displaystyle \ \ \ \ \ \ {{r}^{6}}+1=28$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ {{r}^{6}}\ =27$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ r\ \ =\sqrt{3}\ \ \ \ (\because \alpha >1)$

$ \displaystyle \ \ \ \ \ \ \ \therefore \alpha =\sqrt{3}$

$ \displaystyle {{\log }_{3}}(\frac{3}{2}{{\alpha }^{2}}+{{\alpha }^{4}}+{{\alpha }^{6}}+...+{{\alpha }^{{58}}})$

$ \displaystyle ={{\log }_{3}}(\frac{9}{2}+{{3}^{2}}+{{3}^{3}}+{{3}^{4}}+...+{{3}^{{29}}})$

$ \displaystyle ={{\log }_{3}}(\frac{9}{2}+\frac{{9({{3}^{{28}}}-1)}}{2})$

$ \displaystyle ={{\log }_{3}}\frac{{{{3}^{{30}}}}}{2}$

$ \displaystyle ={{\log }_{3}}{{3}^{{30}}}-{{\log }_{3}}2$

$ \displaystyle =30-{{\log }_{3}}2$

Approximation

Given that $ \displaystyle y=6x\ {{e}^{{3-4x}}}$ and when $ \displaystyle x=\frac{3}{4}$, there is increase in x of k % . Determine, in terms of k , the approximate percentage change in the value of y .

$ \displaystyle y=6x\ {{e}^{{3-4x}}}$

$ \displaystyle \frac{{dy}}{{dx}}=6(x\frac{d}{{dx}}{{e}^{{3-4x}}}+{{e}^{{3-4x}}}\frac{{dx}}{{dx}})$

$ \displaystyle \ \ \ \ \ =6(-4x\ {{e}^{{3-4x}}}+{{e}^{{3-4x}}})$

$ \displaystyle \ \ \ \ \ =6{{e}^{{3-4x}}}(1-4x)$

$ \displaystyle \text{when  }x=\frac{3}{4},\ \ \frac{{dy}}{{dx}}=6\ {{e}^{0}}(-2)=-12$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \delta x=\frac{3}{4}k\text{ }\!\!%\!\!\text{ }$ %

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{3k}}{{400}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \delta y\simeq (\frac{{dy}}{{dx}})\delta x$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \simeq -12(\frac{{3k}}{{400}})$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \simeq -\frac{{9k}}{{100}}$

$ \displaystyle \text{when  }x=\frac{3}{4},\ \ y=\frac{9}{2}$

$\displaystyle \text{Approximate percentage change in }y=\frac{{\delta y}}{y}\times 100\ %$%

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \simeq -\frac{{9k}}{{100}}\times \frac{2}{9}\times 100\ %$%

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \simeq -2k\ \text{ }\!\!%\!\!\text{ }$%

Trigonometry and Quadratic equation

 If $ \displaystyle \sec \theta +\cos ec\ \theta =2$ , find exact value of $ \displaystyle \sin \theta $.

  Solution

$ \displaystyle \sec \theta +\cos ec\ \theta =2$

$ \displaystyle \frac{1}{{\cos \theta }}\ +\ \frac{1}{{\sin \theta }}\ \ =\ 2$

$ \displaystyle \frac{{\sin \theta +\cos \theta }}{{\sin \theta \cos \theta }}=2$

$ \displaystyle \sin \theta +\cos \theta =\sin 2\theta \ \ ......(1)$

$ \displaystyle {{(\sin \theta +\cos \theta )}^{2}}={{\sin }^{2}}2\theta $

$ \displaystyle {{\sin }^{2}}\theta +2\sin \theta \cos \theta +{{\cos }^{2}}\theta ={{\sin }^{2}}2\theta $

$ \displaystyle 1+\sin 2\theta ={{\sin }^{2}}2\theta $

$ \displaystyle {{\sin }^{2}}2\theta -\sin 2\theta -1=0$

$ \displaystyle \sin 2\theta =\frac{{1-\sqrt{5}}}{2}\ \ [\because -1\le {{\sin }^{2}}2\theta \le 1]$

$ \displaystyle 2\sin \theta \cos \theta =\frac{{1-\sqrt{5}}}{2}$

$ \displaystyle \cos \theta =\frac{{1-\sqrt{5}}}{{4\sin \theta }}$

$ \displaystyle \sin \theta +\frac{{1-\sqrt{5}}}{{4\sin \theta }}=\frac{{1-\sqrt{5}}}{2}\ \ \ \ \ [\ By\ (1)\ ]$

$ \displaystyle 4{{\sin }^{2}}\theta +1-\sqrt{5}=(2-2\sqrt{5})\sin \theta $

$ \displaystyle 4{{\sin }^{2}}\theta -(2-2\sqrt{5})\sin \theta +1-\sqrt{5}=0$

$ \displaystyle \sin \theta =\frac{{2-2\sqrt{5}\pm \sqrt{{{{{(2-2\sqrt{5})}}^{2}}-16(1-\sqrt{5})}}}}{8}$

$ \displaystyle \ \ \ \ \ \ \ =\frac{{2-2\sqrt{5}\pm \sqrt{{8+8\sqrt{5}}}}}{8}$

$ \displaystyle \ \ \ \ \ \ \ =\frac{{2-2\sqrt{5}\pm 2\sqrt{{2+2\sqrt{5}}}}}{8}$

$ \displaystyle \ \ \ \ \ \ \ =\frac{{1-\sqrt{5}\pm \sqrt{{2+2\sqrt{5}}}}}{4}$

Solving problem with basic trigonometry formula

 Prove that $ \displaystyle \frac{2}{{1+\sin x+\cos x}}=\frac{{\sin x}}{{1+\cos x}}+\frac{{\cos x}}{{1+\sin x}}$.


$ \displaystyle \frac{2}{{1+\sin x+\cos x}}=\frac{{2(\sin x+\cos x-1)}}{{{{{\sin }}^{2}}x+2\sin x\cos x+{{{\cos }}^{2}}x-1}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{2(\sin x+\cos x-1)}}{{2\sin x\cos x}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\sin x+\cos x-{{{\sin }}^{2}}x-{{{\cos }}^{2}}x}}{{\sin x\cos x}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\cos x(1-\cos x)+\sin x(1-\sin x)}}{{\sin x\cos x}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{1-\cos x}}{{\sin x}}+\frac{{1-\sin x}}{{\cos x}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{1-{{{\cos }}^{2}}x}}{{\sin x(1+\cos x)}}+\frac{{1-{{{\sin }}^{2}}x}}{{\cos x(1+\sin x)}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{{{{\sin }}^{2}}x}}{{\sin x(1+\cos x)}}+\frac{{{{{\cos }}^{2}}x}}{{\cos x(1+\sin x)}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\sin x}}{{1+\cos x}}+\frac{{\cos x}}{{1+\sin x}}$

Solving problem with some basic trigonometry formula and factor formula

 ABC is a triangle such that $ \displaystyle {{\sin }^{2}}A+{{\sin }^{2}}B+{{\sin }^{2}}C=2$ ,
show that $ \displaystyle \Delta \ ABC$ is a right triangle .

$ \displaystyle {{\sin }^{2}}A+{{\sin }^{2}}B+{{\sin }^{2}}C=2\ \ ......(1)$

$ \displaystyle {{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=1\ ......(2)$

$ \displaystyle (2)-(1)\Rightarrow $

$ \displaystyle {{\cos }^{2}}A-{{\sin }^{2}}A+{{\cos }^{2}}B-{{\sin }^{2}}B+{{\cos }^{2}}C-{{\sin }^{2}}C=-1$

$ \displaystyle \cos 2A+\cos 2B+\cos 2C=-1$

$ \displaystyle 2\cos (A+B)\cos (A-B)+2{{\cos }^{2}}C-1=-1$

$ \displaystyle 2\cos ({{180}^{\circ }}-C)\cos (A-B)+2{{\cos }^{2}}C=0$

$ \displaystyle -2\cos C\cos (A-B)+2{{\cos }^{2}}C=0$

$ \displaystyle 2\cos C\left[ {\cos C-\cos (A-B)} \right]=0$

$ \displaystyle -4\cos C\sin \frac{{C+A-B}}{2}\sin \frac{{C+B-A}}{2}=0$

$ \displaystyle \cos C\sin \frac{{{{{180}}^{\circ }}-2B}}{2}\sin \frac{{{{{180}}^{\circ }}-2A}}{2}=0$

$ \displaystyle \cos C\sin ({{90}^{\circ }}-B)\sin ({{90}^{\circ }}-A)=0$

$ \displaystyle \cos C\cos B\cos A=0$

$ \displaystyle \cos A=0\ \ \ (\text{or})\ \ \ \cos B=0\ \ \ (\text{or})\ \ \ \cos C=0$

$ \displaystyle \ \ \ \ \ A={{90}^{\circ }}\ (\text{or})\ \ \ \ \ B={{90}^{\circ }}\ \ (\text{or})\ \ \ \ \ \ \ \ C={{90}^{\circ }}$

$ \displaystyle \therefore \Delta \ ABC\ $ is a right triangle .

Compound angle formula Vs Componendo and dividendo

 If $ \displaystyle \frac{{m+1}}{{m-1}}=\frac{{\cos (\alpha -\beta )}}{{\sin (\alpha +\beta )}}$ , prove that $ \displaystyle \ \ \ m=\tan (\alpha +{{45}^{\circ }})\tan (\beta +{{45}^{\circ }})$


$ \displaystyle \frac{{m+1}}{{m-1}}=\frac{{\cos (\alpha -\beta )}}{{\sin (\alpha +\beta )}}$

$ \displaystyle \frac{{m+1}}{{m-1}}=\frac{{\cos \alpha \cos \beta +\sin \alpha \sin \beta }}{{\sin \alpha \cos \beta +\cos \alpha \sin \beta }}$

By Componendo and Dividendo ,

$ \displaystyle \frac{{2m}}{2}=\frac{{\cos \alpha \cos \beta +\sin \alpha \sin \beta +\sin \alpha \cos \beta +\cos \alpha \sin \beta }}{{\cos \alpha \cos \beta +\sin \alpha \sin \beta -\sin \alpha \cos \beta -\cos \alpha \sin \beta }}$

$ \displaystyle m=\frac{{\cos \beta (\sin \alpha +\cos \alpha )+\sin \beta (\sin \alpha +\cos \alpha )}}{{\cos \beta (\cos \alpha -\sin \alpha )-\sin \beta (\cos \alpha -\sin \alpha )}}$

$ \displaystyle \ \ \ =\frac{{(\sin \alpha +\cos \alpha )(\sin \beta +\cos \beta )}}{{(\cos \alpha -\sin \alpha )(\cos \beta -\sin \beta )}}$

$ \displaystyle \ \ \ =\frac{{\tan \alpha +1}}{{1-\tan \alpha }}\times \frac{{\tan \beta +1}}{{1-\tan \beta }}$

$ \displaystyle \ \ \ =\frac{{\tan \alpha +\tan {{{45}}^{\circ }}}}{{1-\tan \alpha \tan {{{45}}^{\circ }}}}\times \frac{{\tan \beta +\tan {{{45}}^{\circ }}}}{{1-\tan \beta \tan {{{45}}^{\circ }}}}$

$ \displaystyle \ \ \ =\tan (\alpha +{{45}^{\circ }})\tan (\beta +{{45}^{\circ }})$

Compound angle formula Vs Triple angle

 Prove that $ \displaystyle \cot (\alpha +\beta )=\frac{{\cot \alpha \cot \beta -1}}{{\cot \alpha +\cot \beta }}$ and hence prove that $ \displaystyle \cot \theta +\cot ({{60}^{\circ }}+\theta )-\cot ({{60}^{\circ }}-\theta )=3\cot 3\theta $ .


$ \displaystyle \cot (\alpha +\beta )=\frac{1}{{\tan (\alpha +\beta )}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{1-\tan \alpha \tan \beta }}{{\tan \alpha +\tan \beta }}$

$ \displaystyle \ \ \ \ \ \ \ \,\ \ \ \ \ \ \ \ =\frac{{1-\frac{1}{{\cot \alpha \cot \beta }}}}{{\frac{1}{{\cot \alpha }}+\frac{1}{{\cot \beta }}}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\frac{{\cot \alpha \cot \beta -1}}{{\cot \alpha \cot \beta }}}}{{\frac{{\cot \beta +\cot \alpha }}{{\cot \alpha \cot \beta }}}}$

$ \displaystyle \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\cot \alpha \cot \beta -1}}{{\cot \beta +\cot \alpha }}$

$ \displaystyle \cot \theta +\cot ({{60}^{\circ }}+\theta )-\cot ({{60}^{\circ }}-\theta )$

$ \displaystyle =\cot \theta +\frac{{\cot {{{60}}^{\circ }}\cot \theta -1}}{{\cot {{{60}}^{\circ }}+\cot \theta }}-\frac{{\cot {{{60}}^{\circ }}\cot \theta +1}}{{\cot \theta -\cot {{{60}}^{\circ }}}}$

$ \displaystyle =\cot \theta +\frac{{\frac{1}{{\sqrt{3}}}\cot \theta -1}}{{\frac{1}{{\sqrt{3}}}+\cot \theta }}-\frac{{\frac{1}{{\sqrt{3}}}\cot \theta +1}}{{\cot \theta -\frac{1}{{\sqrt{3}}}}}$

$ \displaystyle =\cot \theta +\frac{{\cot \theta -\sqrt{3}}}{{1+\sqrt{3}\cot \theta }}-\frac{{\cot \theta +\sqrt{3}}}{{\sqrt{3}\cot \theta -1}}$

$ \displaystyle =\cot \theta +\frac{{\sqrt{3}{{{\cot }}^{2}}\theta -\cot \theta -3\cot \theta +\sqrt{3}-\cot \theta -\sqrt{3}-\sqrt{3}{{{\cot }}^{2}}\theta -3\cot \theta }}{{3{{{\cot }}^{2}}\theta -1}}$

$ \displaystyle =\cot \theta -\frac{{8\cot \theta }}{{3{{{\cot }}^{2}}\theta -1}}$

$ \displaystyle =\frac{{3{{{\cot }}^{3}}\theta -9\cot \theta }}{{3{{{\cot }}^{2}}\theta -1}}$

$ \displaystyle \cot 2\theta =\frac{{{{{\cot }}^{2}}\theta -1}}{{2\cot \theta }}$

$ \displaystyle \cot 3\theta =\cot (2\theta +\theta )$

$ \displaystyle \ \ \ \ \ \ \ \ \ =\frac{{\cot 2\theta \cot \theta -1}}{{\cot 2\theta +\cot \theta }}$

$ \displaystyle \ \ \ \ \ \ \ \ \ =\frac{{(\frac{{{{{\cot }}^{2}}\theta -1}}{{2\cot \theta }})\cot \theta -1}}{{\frac{{{{{\cot }}^{2}}\theta -1}}{{2\cot \theta }}+\cot \theta }}$

$ \displaystyle \ \ \ \ \ \ \ \ \ =\frac{{{{{\cot }}^{3}}\theta -\cot \theta -2\cot \theta }}{{{{{\cot }}^{2}}\theta -1+2{{{\cot }}^{2}}\theta }}$

$ \displaystyle \ \ \ \ \ \ \ \ \ =\frac{{{{{\cot }}^{3}}\theta -3\cot \theta }}{{3{{{\cot }}^{2}}\theta -1}}$

$ \displaystyle 3\cot 3\theta =\frac{{3{{{\cot }}^{3}}\theta -9\cot \theta }}{{3{{{\cot }}^{2}}\theta -1}}$

$ \displaystyle \therefore \cot \theta +\cot ({{60}^{\circ }}+\theta )-\cot ({{60}^{\circ }}-\theta )=3\cot 3\theta $

Compound angle Vs Double angle Vs Componendo and Dividendo

2. Prove that  $ \displaystyle \cos 2\theta =\frac{{1+{{{\tan }}^{2}}\theta }}{{1+{{{\tan }}^{2}}\theta }}$ . Hence prove that $ \displaystyle \cos 2\theta =\frac{{m+n}}{{2(m-n)}}$ given that $ \displaystyle m\tan (\theta -\frac{\pi }{6})=n\tan (\theta +\frac{{2\pi }}{3})$ .

$ \displaystyle \begin{array}{l}\cos 2\theta ={{\cos }^{2}}\theta -{{\sin }^{2}}\theta \\\ \ \ \ \ \ \ \ \ \ =\frac{{{{{\cos }}^{2}}\theta -{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta +{{{\sin }}^{2}}\theta }}\\\ \ \ \ \ \ \ \ \ \ =\frac{{1-\frac{{{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}}}{{1+\frac{{{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{2}}\theta }}}}\\\ \ \ \ \ \ \ \ \ \ =\frac{{1-{{{\tan }}^{2}}\theta }}{{1+{{{\tan }}^{2}}\theta }}\\m\tan (\theta -\frac{\pi }{6})=n\tan (\theta +\frac{{2\pi }}{3})\\m(\frac{{\tan \theta -\tan {{{30}}^{\circ }}}}{{1+\tan \theta \tan {{{30}}^{\circ }}}})=n(\frac{{\tan \theta +\tan {{{120}}^{\circ }}}}{{1-\tan \theta \tan {{{120}}^{\circ }}}})\\m(\frac{{\tan \theta -\frac{1}{{\sqrt{3}}}}}{{1+\frac{1}{{\sqrt{3}}}\tan \theta }})=n(\frac{{\tan \theta -\sqrt{3}}}{{1+\sqrt{3}\tan \theta }})\\m(\frac{{\sqrt{3}\tan \theta -1}}{{\sqrt{3}+\tan \theta }})=n(\frac{{\tan \theta -\sqrt{3}}}{{1+\sqrt{3}\tan \theta }})\\\frac{m}{n}=\frac{{\tan \theta -\sqrt{3}}}{{1+\sqrt{3}\tan \theta }}\times \frac{{\sqrt{3}+\tan \theta }}{{\sqrt{3}\tan \theta -1}}\\\frac{m}{n}=\frac{{{{{\tan }}^{2}}\theta -3}}{{3{{{\tan }}^{2}}\theta -1}}\\\frac{{m+n}}{{m-n}}=\frac{{4{{{\tan }}^{2}}\theta -4}}{{-2{{{\tan }}^{2}}\theta -2}}\left[ {By\ Componendo\ and\ Dividendo} \right]\\\frac{{m+n}}{{m-n}}=\frac{{2(1-{{{\tan }}^{2}}\theta )}}{{1+{{{\tan }}^{2}}\theta }}\\\frac{{m+n}}{{2(m-n)}}=\frac{{1-{{{\tan }}^{2}}\theta }}{{1+{{{\tan }}^{2}}\theta }}\\\therefore \ \ \cos 2\theta =\frac{{m+n}}{{2(m-n)}}\end{array}$

Compound angle formula Vs Double angle formula

 Prove that $ \displaystyle \frac{{\cos 3A+\sin 3A}}{{\cos A-\sin A}}=1+2\sin 2A$ .

$ \displaystyle \begin{array}{l}\frac{{\cos 3A+\sin 3A}}{{\cos A-\sin A}}=\frac{{\cos (2A+A)+\sin (2A+A)}}{{\cos A-\sin A}}\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\cos 2A\cos A-\sin 2A\sin A+\sin 2A\cos A+\cos 2A\sin A}}{{\cos A-\sin A}}\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{\cos 2A(\cos A+\sin A)+\sin 2A(\cos A-\sin A)}}{{\cos A-\sin A}}\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{{({{{\cos }}^{2}}A-{{{\sin }}^{2}}A)(\cos A+\sin A)}}{{\cos A-\sin A}}+\sin 2A\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ={{(\cos A+\sin A)}^{2}}+\sin 2A\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ={{\cos }^{2}}A+2\sin A\cos A+{{\sin }^{2}}A+\sin 2A\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =1+\sin 2A+\sin 2A\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =1+2\sin 2A\end{array}$

Maths Problems & Solutions (1)